Materiały
na kolokwium
z Ekonometrii
WSPÓŁCZYNNIK PEARSONA
W przypadku współczynnika Pearsona sprawa w zasadzie jest dość prosta jest tylko jeden wzór
z którego należy skorzystać, aby wyznaczyć współczynnik i odpowiednio go zinterpretować
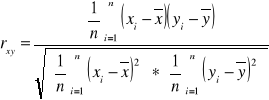
n - liczba elementów
![]()
- wartości średnie
Rozwiązanie polega na wypełnieniu wartości w tabeli
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
i |
X |
Y |
|
|
|
|
|
wartości w kolumnach 1,2 i 3 są podane
obliczamy dodając do siebie wszystkie xi i dzieląc przez n
obliczamy dodając do siebie wszystkie yi i dzieląc przez nsumujemy wyniki z kolumny 6
sumujemy wyniki z kolumny 7
sumujemy wyniki z kolumny 8
wszystko podstawiamy do wzoru
Interpretacja wyniku:
jeżeli
- zależność dodatniajeżeli
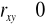
- zależność ujemnajeżeli
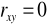
- brak zależności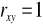
lub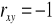
- silna zależność liniowa
Model ekonometryczny
Macierz współczynników korelacji
W pierwszym momencie można się załamać jak się na to spojrzy, ale może „w tym szaleństwie jest metoda”
W zadaniu otrzymujemy macierz R ( symetryczną - na przekątnej same jedynki ) i R0. Zgodnie z ustaleniami wartość krytyczna r* także będzie podana, więc wzór na jej wyliczanie pominę.
Warto pamiętać o dwóch zależnościach
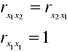
Przykład rozwiązania
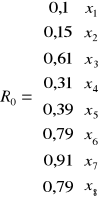
r*=0,6
Krok 1
![]()
z tabeli R0 wyrzucamy zmienne które spełniają powyższy warunek czyli ![]()
są to:
x1,x2,x4,x5
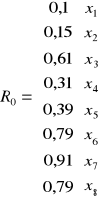
Krok 2
Z tablicy R0 wybieramy najwyższą wartość czyli x7=0,91 i nazywamy ją xh
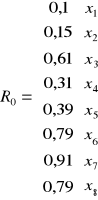
Krok 3
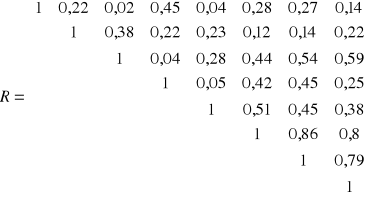
xh dotyczyło wartości x7 dlatego sprawdzamy wartości w 7 kolumnie macierzy R. Po usunięciu wartości w kroku 1 pozostały nam wartości x3,x6,x7,x8 współczynniki stojące przy x-ach oznaczają wiersze które będą nas interesować
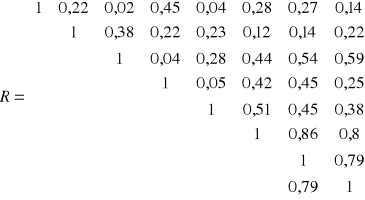
xh=x7
x3 - wartość znajdująca się na przecięciu 7 kolumny i 3 wiersza![]()
wynosi 0,54
x6 - wartość znajdująca się na przecięciu 7 kolumny i 6 wiersza ![]()
wynosi 0,86
x8 - wartość znajdująca się na przecięciu 7 kolumny i 8 wiersza ![]()
wynosi 0,79
Krok 4
![]()
Sprawdzamy które z wartości wybranych w poprzednim kroku spełniają warunki powyższego wzoru i te eliminujemy z modelu.
Krok 5
Do modelu wchodzą zmienne ![]()
oraz x7
Model wygląda więc następująco
![]()
Metoda współczynników
informacyjnych Hellwiga
W tej metodzie mamy dane tylko R i R0
Rozpatrujemy wszystkie możliwe kombinacje potencjalnych zmiennych objaśniających. Ilość kombinacji obliczamy ze wzoru
![]()
m - liczba zmiennych objaśniających
Wskaźnik indywidualny
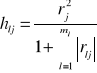
Jako, że ![]()
dla ułatwienia wskaźnik indywidualny można zapisać następująco
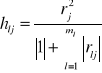
Dla l=j powyższy wzór ma postać
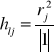
Przykład rozwiązania
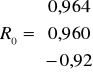
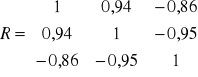
Krok 1
Obliczamy i wypisujemy wszystkie kombinacje potencjalnych zmiennych objaśniających
![]()
kombinacji x1, x2, x3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Krok 2
![]()
W przypadku kombinacji K1 w macierzy R rozpatrujemy liczbę znajdującą się w 1 wierszu i w 1 kolumnie. Jako, że wartość w macierzy R znajduje się w 1 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 1 wierszu
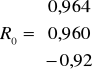
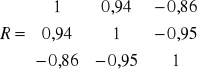
Wartość współczynnika indywidualnego dla kombinacji K1 wynosi 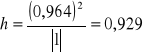
Krok 3
![]()
W przypadku kombinacji K2 w macierzy R rozpatrujemy liczbę znajdującą się w 2 wierszu i w 2 kolumnie. Jako, że wartość w macierzy R znajduje się w 2 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 2 wierszu
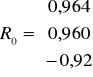
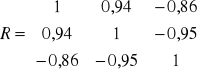
Wartość współczynnika indywidualnego dla kombinacji K2 wynosi 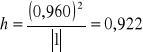
Krok 4
![]()
W przypadku kombinacji K3 w macierzy R rozpatrujemy liczbę znajdującą się w 3 wierszu i w 3 kolumnie. Jako, że wartość w macierzy R znajduje się w 3 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 3 wierszu
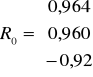
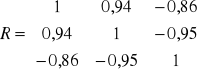
Wartość współczynnika indywidualnego dla kombinacji K3 wynosi 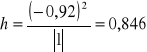
Krok 5
![]()
W przypadku kombinacji K4 w macierzy R rozpatrujemy pierwsze dwie liczby znajdujące się w 1 wierszu i pierwsze dwie w liczby znajdujące się w 2 wierszu. Jako, że wartości w macierzy R znajduje się w 1 i 2 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 1 i 2 wierszu
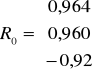
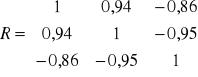
Można przyjąć, że dla kombinacji K4 macierz R i R0 wygląda następująco
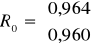
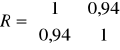
Wartość współczynnika indywidualnego dla kombinacji K4 w 1 wierszu wynosi 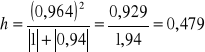
Wartość współczynnika indywidualnego dla kombinacji K4 w 2 wierszu wynosi 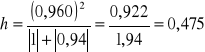
Krok 6
![]()
W przypadku kombinacji K5 w macierzy R rozpatrujemy ostatnie dwie liczby znajdujące się w 2 wierszu i ostatnie dwie w liczby znajdujące się w 3 wierszu. Jako, że wartości w macierzy R znajduje się w 2 i 3 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 2 i 3 wierszu
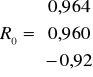
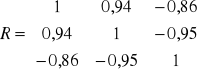
Można przyjąć, że dla kombinacji K5 macierz R i R0 wygląda następująco
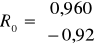
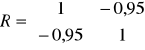
Wartość współczynnika indywidualnego dla kombinacji K5 w 2 wierszu wynosi 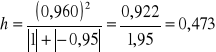
Wartość współczynnika indywidualnego dla kombinacji K5 w 2 wierszu wynosi 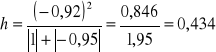
Krok 7
![]()
W przypadku kombinacji K6 w macierzy R rozpatrujemy pierwszą i trzecią liczbę znajdującą się w 1 i 3 wierszu. Jako, że wartości w macierzy R znajduje się w 1 i 3 wierszu to w macierzy R0 także interesuje nas to co znajduje się w 1 i 3 wierszu
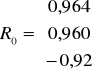
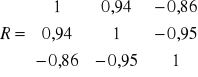
Można przyjąć, że dla kombinacji K6 macierz R i R0 wygląda następująco
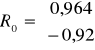
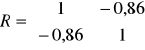
Wartość współczynnika indywidualnego dla kombinacji K5 w 1 wierszu wynosi 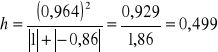
Wartość współczynnika indywidualnego dla kombinacji K5 w 3 wierszu wynosi 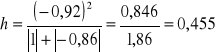
Krok 8
![]()
W przypadku kombinacji K7 rozpatrujemy całą macierz R i całą macierz R0
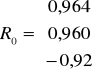
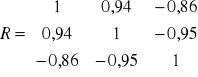
Wartość współczynnika indywidualnego dla kombinacji K7 w 1 wierszu wynosi 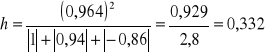
Wartość współczynnika indywidualnego dla kombinacji K7 w 2 wierszu wynosi 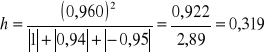
Wartość współczynnika indywidualnego dla kombinacji K7 w 3 wierszu wynosi 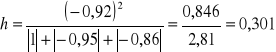
Krok 9
Integralny wskaźnik pojemności informacyjnej
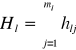
Dla poszczególnych kombinacji integralny wskaźnik pojemności informacyjnej jest sumą współczynników indywidualnych dla poszczególnych wierszy macierzy
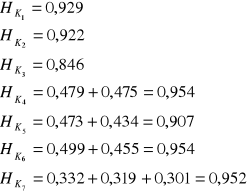
Do modelu należą zmienne należące do kombinacji dla której H jest maksymalny
Powyższy przykład nie rozstrzyga jednoznacznie, dlatego do modelu należą ![]()
i ![]()
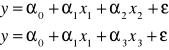
Eliminacja zmiennych quasi-stałych
V* - wartość krytyczna ( będzie dana )
Dla każdej zmiennej objaśniającej xi wyznaczamy współczynnik zmienności
Obliczamy Vi ze wzoru
![]()
Z modelu wyłączamy zmienne spełniające warunek
![]()
Model ekonometryczny liniowy
z jedną zmienną
Korzystamy ze wzorów
Wyliczamy średnią ![]()
![]()
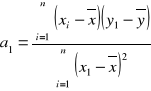
![]()
Wyliczamy wartości w tabeli i podstawiamy do wzorów
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
wartości w kolumnach 1,2,3 są podane
sumujemy wartości w kolumnie 6
sumujemy wartości w kolumnie 7
Wszystko podstawiamy do wzoru
Korzystając z własności macierzy symetrycznej wiemy, że wartość przecięcia 7 kolumny z 8 wierszem ma taką samą wartość jak przecięcie 8 kolumny z 7 wierszem
Uwaga tego nie jestem na 100% pewien, bo w notatkach miałem trochę namieszane
uwaga, ten wzór to moja własna interpretacja, więc każdy używa go na własne ryzyko
zrezygnowałem z indeksów przy oznaczeniu współczynnika indywidualnego h gdyż dla mnie był trochę mylący
Do modelu zawsze wchodzi xh
Wyszukiwarka
Podobne podstrony:
zadania przygotowujace na kolokwium, materiały ekonomia UWM, Statystyka
J. Huizinga - Jesień średniowiecza, Notatki, opracowania, materiały na kolokwia
Zakres materiału obowiązującego na kolokwium
ZAKRES MATERIAŁU OBOWIAZUJACEGO NA KOLOKWIUM, STOMATOLOGIA, Fizjo Żucia
pytania tple, materiały farmacja, materiały V rok, TPL, do zaliczenia, na kolokwium
Zakres materiału obowiązujący na II kolokwium wykładowe, Chemia ogólna i nieorganiczna, giełdy
Napęd elektryczny materiał na kolokwium
zzl ćwiczenia materiały na kolokwium
ekonometria, PRZYKŁADOWE ZADANIA NA KOLOKWIUM Z EKONOMETRII
Zarządzanie projektami ekonomicznymi i organizacyjnym Materiały na egzamin
Zakres materiału na kolokwium z biomedycznych (1)
materialy na kolokwium (1)
Materiał na kolokwium z wprowadzenia do pedagogiki (1)
Historii Maniaków streszczenie, Notatki, opracowania, materiały na kolokwia
Zakres materiału i zagadnienia na kolokwium 1 z Układów elektronicznych
Zakres materiału na kolokwia i ich planowane terminy, Zakres materiału na kolokwia i ich planowane t
Materiały na kolokwium II
więcej podobnych podstron