60657

ł_n wartość wyznaczana na podstawie rozkładu t-Studenta o n-1 stopniach swobody : parametr ten wyznaczamy za pomocą funkcji ROZ* KŁAD.T.ODW:

uwaga! jako prawdopodobieństwo podajemy o. a jako liczbę stopni swobody podajemy liczbę prób MINUS JEDEN

y/ti pierwiastek z liczby prób: wyznaczamy funkcją PIER\VIASTEK(liczba prób)

Wówczas przedział ufności wygląda następująco:

Dolna granica:    Górna granica:

1.2.2 Duża liczba prób (« > 30)

Przedział ufności wyznacza się ze wzoru:

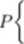
= l-o

x — u„ —= < m < x + u„ —= y/n    y/n

Objaśnienia:

(uwaga! \\%* wzorze nastąpiła wyłącznie zmiana parametru t„ na u„)

m„ wartość wyznaczana na podstawie rozkładu nornialnego standaryzowanego jV(0.1):

w Excełu jest to funkcja ROZKLAD.NORMALNY.S.ODW: uwaga! jako parametr tej funkcji podajemy 1 — a/2

Przedział ufności:

Dolna granica:    Górna granica:

UWAGA! w nowszych wersjach Excela istnieje funkcja UFNOŚĆ(alfa:odch.std;rozmiar), która upraszcza obliczanie przedziałów. ALE TYLKO DLA DUŻEJ PRÓBY.

Lewy kraniec przedziału to l—UFNOŚC(o;»;n), a prawy to x+UFNOŚĆ(a: ś; n)

1.3 Przedział ufności dla wariancji i odchylenia standardowego

1.3.1 Mała liczba prób (n < 30)

Przy małej liczbie prób wyznaczamy najpierw przedział ufności dla wariancji. Granice przedziału ufności dla odchylenia standardowego wyznaczamy jako pierwiastki granic przedziału ufn. dla wariancji. Stąd odpowiednio wykorzystujemy

2