60725

Układy równań liniowych

Dokładne metody rozwiązywania układów równań liniowych

Jeżeli rozwiązanie układu równań AX=tł polega na takim przekształceniu macierzy /I i W. że przy założeniu dokładnie wykonywanych działali arytmetycznych po skończonej liczbie działań otrzymujemy ro/wiązanic, to taką metodę n>zw iązania nazywamy metodą dokładną.

Pomijamy wzory Cramera. schemat Sarmsa ilti. Stosując metodę Cramera rude ty obliczyć ln+11 wyznaćznikiru. które wymagają co najmniej tn*l)! mnoteil Jest to więc metoda bardzo pracochłonna i dlatego jej się nie stosuje dla n>4.

I) A jest macierzą diagonalną.

a„ 0 . . 0		*1		/>,
0 a.. . . 0				b.
			■	■
0 0 . .

Rozwiązanie nu postać:    x, =

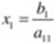
itd...

A.

a ^

Układy równań liniowych

2) macierz A jest macierzą trójkątną górną (algorytm .podstawiania wstecz")'-

	^a.l •	• ^aiu		^xi
0	022 •	• a}M				*
			•	•	“	•
0	0 .	• am				bu.

Ucz ba operacji: 7t<N>*N) mnożeń i dzieleń VHN*+N) dodawań

Kłopot, ply Hornem jfcSwny a,<J)

-a

^XS-2

N-2N~M

^au-2N-2

x,=-^-i = N-\.N

^au

Napisać samodzielnie algorytm .podstawiania w przód’(dla macierzy trójkątnej dolnej)