65528

ROZCIĄGANIE PRĘTÓW PROSTYCH 2

2.2. Podejście statyczne do zagadnienia brzegowego

	"wymyślić” Tc sprawdzić staL war. brzeg, sprawdzić równ. Naviera
	wyznaczyć odkształcenia e..= e..(a.) ij ij^v if sprawdzić równ. nierozdz. odkszt.
	wyznaczyć przemieszczenia
	^eii =2 ^(ui.i ^+ ui.i) + kinematyczne war. brzegowe
V

* - macierz naprężenia

S W|] = S(Z,| M( W|| = Ml Zij

q 0 0

T_c = 0 0 0 000

Macierz naprężenia (6) spełnia równania równowagi (1) i statyczne warunki brzegowe (4) * - macierz odkształceń (r.Hooke'a)

e

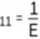
C 22

(6)

1+ v ( 0 n - VI 0 u+ 0 22+ 0 33 =|q

0 22 ~ V ! 011*022 + 033!

£33 = “ (l+v|033 -v(0u+022 + 0»||^s-|q

| [ 11+ v | 0 12	= 0
PO w II PO 3 II 0
'1/E O	O
0 1 4 m	O
0 0 1	v/E

(7)

Macierz (7) spełnia równania nierozdzielności odkształceń, gdyż

«ij = const a tpsO

* - funkcje przemieszczeń (rów. Cauch/ego)

aui = q	aui + au2 =0
3xi " E	9X2 9Xi
	au2 + au3 =0
X ro m	9x3 9x2
	W w II 0
dx3 E	9x3 9xi

Ukł. (8) to układ 6 równań różniczkowych cząstkowych liniowych I rzędu

"CORN" = "CORJ" + "CSRN" => Uj = U° + Up

(8)