72052

prawami optyki geometrycznej (kąt odbicia = kątowi padania). Schemat takiego odbicia pokazano na rys. 2.

Rys.2. Schemat odbicia promieni rentgenowskich od dwóch równoległych płaszczyzn atomowych.

Odbicie promieni rentgenowskich (czyli fal elekromagnetycznych o długościach fali porównywalnych z odległościami międzyatomowymi) od pojedynczej płaszczyzny atomów jest o wiele za słabe aby mogło zostać zaobserwowane doświadczalnie. Jednak w przypadku gdy odbicia od 2, 3 i kilkuset następnych równoległych płaszczyzn krystalograficznych nałożą się na siebie „w zgodnej fazie” sumaryczna fala odbita będzie na tyle silna, że spowoduje wyraźnie mierzalny efekt nazywany często odbiciem interferencyjnym lub odbiciem Bragga.

Warunki jakie muszą być spełnione aby efekt ten wystąpił zostały po raz pierwszy podane przez Bragga w 1913r i noszą nazwę prawa Bragga:

2d sin(D ) 0 n D    (1)

gdzie:

d - odległość między sąsiednimi płaszczyznami atomowymi 0- kąt dyfrakcji (patrz rys.2)

D - długość fali promieniowania rentgenowskiego n - liczba naturalna

Jednym z ważnych wniosków wynikających z tego równania jest ogólny warunek na długość fal promieniowania rentgenowskiego jaka może być stosowana w badaniach dyfraktometrycznych. Ponieważ sin(0) jest zawsze D 1 zaś n D 1 aby uzyskać jakiekolwiek odbicie dyfrakcyjne od kryształu długość fali musi spełniać warunek:

00 2dmax    (2)

gdzie dmax oznacza największą odległość między sąsiadującymi płaszczyznami sieciowymi badanego kryształu. Ponieważ wymiary komórek elementarnych kryształów są rzędu kilku angstremów (1A =10-10 m) tego samego rzędu muszą być również stosowane długości fal rentgenowskich.

Aparatura badawcza:

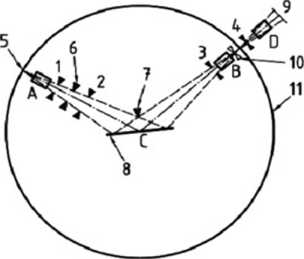
Rys. 5. Schemat dyfraktometru rentgenowskiego o geometrii Bragg-Brentano:

1, 2, 3, 4 - szczeliny antyrozproszeniowe, 5 - punkt wejścia promieniowania (pozorne źródło), 6 - szczelina kontrolująca rozbieżność wiązki, 7 - ostrze, 8 - płaska próbka,

9 - okienko detektor promieniowania, 10 - szczelina odbiorcza, 11 - koło goniometru, A, B, D - szczeliny Sollera, oś próbki i goniometru.