73695

v\Uad III

F(x)=P(X±x)=\ttt)dt

Interpretacja geometryczna dystrybuanty na wykresie funkcji gęstości/(.v): dystrybuanta w punkcie xjest polem pod gęstością na lewo od wartości x

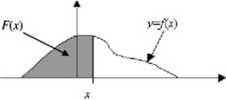
Dystrybuanta jest funkcją ciągłą, niemalejącą, ^ f^-00)^— 0 ; b (°°) — I. Jeśli znamy dystrybuantę to można obliczyć:

1.    gęstość f(^x)⁼ F C^v) (w punktach ciągłości f{x))

2.    prawdopodobieństwo P(^a < X <b) = F(b) — F(a)

Obliczanie prawdopodobieństw

	mając gęstość flx)	mając dystrybuantę FM
p(x < a)	= j f{x)dx	= F(a)
P(X >b)	= jf(x)dx b	= 1 ~F(b)
P(a < X < b)	b = J7W* a	= F(b)-F(a)

2