82305

Przykład 7.3 Rozpatrzmy przykłady zagadnień początkowych:

o)

y = c

0(0) = 2

6) ( ^y' = ²^ ' 1 0(0) = 0

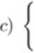
0' = f(y) y(0) = -i

. gdzie f{y) =

{

y ln y dla y > 0 0 dla y = 0

Rozwiązanie zagadnienia Cauchy’ego dla równania pierwszego rzędu (*) polega na znalezieniu rozwiązania tego równania w pewnym przedziale / C R-. które s|)ełnia warunek początkowy (**)•

Istnieją równania różniczkowe, które nie mają rozwiązań.

Jeżeli równanie posiada rozwiązanie, to nic zawsze istnieje takie, które spełnia z góry zmiany warunek początkowy (c). Ponadto może się zdarzyć, że Istnieją różne rozwiązania jednego równania różniczkowego, spełniające ten sam warunek początkowy (b).

Twierdzenie 7.1 (Istnienie i jednoznaczość rozwiązania zagadnienia Cauchy’ego)

Jeżeli funkcja f : D —* V, i jej pochodna ^ są ciągle na pewnym obszarze D C Ił² oraz (x₀.0o) € D. to zagadnienie Cauchy’ego

f !/= f(x,y)

\ V(^xo) = 00

ma dokładnie jedno rozuńązanic.

Uwaga 7.2 Inaczej mówiąc, dla dowolnego punktu (xo<0o) € D istnieje dokładnie jedna krzywa całkowa przechodząca przez ten punkt.

Przykład 7.4 Korzystając z podanego wyżej twierdzenia uzasadnić, że wskazane zagadnienia początkowe mają jednoznaczne rozwiązania:

n\ f ^xV + 0² = ⁰ _h\ f ^rf0 = \/0 “ ^xdx v / y' - 0ctgx = sinx ^,\0(1) = 1    ^] \0(1) = 2    ^C)\y(§) = §

7.3 Metody rozwiązywania niektórych równań różniczkowych pierwszego rzędu

1. Równanie o zmiennych rozdzielonych

Definicja 7.4 (Równanie o zmiennych rozdzielonych)

Równanie różniczkowe, które można zapisać w postaci:

y' = y(^x)h(y)

nazywamy równaniem o zmiennych rozdzielonych.

Twierdzenie 7.2 (Rozwiązanie równania o zmiennych rozdzielonych)

Jeżeli funkcje g, h są ciągle, przy czym h(y) £ 0 dla każdego y, to rozwiązanie równania różniczkowego o zmiennych rozdzielonych określone jest zależnością:

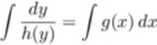
48