82382

Część 1 7. TWIERDZENIA O WZAJEMNOŚCI 3

Układ poddamy działaniu dwóch typów obciążenia i zbadamy przemieszczenia:

•    typ I: działa siła jednostkowa P,-l (w punkcie i), badamy pizemieszczenia w punkcie k (6_b ),

•    typ II: działa siła jednostkowa Pt=l (w punkcie k), mierzymy przemieszczenie w punkcie i ( 6* ). Pomiędzy przemieszczeniami i zachodzi szczegóhiy związek. Pokażemy to na dwóch przykładach.

Przykład 1

Analizie zostaną poddane pizemieszczenia w belce wolnopodpartej.

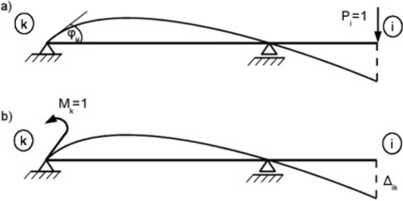
Rys. 7.3. Do belki zastoje: o) przybżono jednostkowa siki, b) przyłotony jednostkowy moment

Do danej belki pizykładamy kolejno jednostkowe obciążenia: w punkcie/ jednostkową siłę P,=l, a w punkcie Ar jednostkowy moment A/*=7. Spowoduje to powstanie odpowiednich przemieszczeń <p_b i dt.

Koizystając z twierdzenia Bettiego można zapisać zależność:

P,A,_k=M_k<ł>_b    (7.4)

Należy zwrócić uwagę na to, że teraz przesunięcie A_k, we wzorze (7.3) ma wartość kąta <P_b w mierze łukowej.

Przyjmując, że układy sił obciążającyclr są jednostkowe, zapis można uprościć:

(7-5)

=</>*

Przykład 2

Do kratownicy przyłożono siłę jednostkową w piuikcie /, która wywołała przemieszczenie w^r piuikcie 2. Następnie do tej samej kratownicy przyłożono siłę jednostkową w punkcie.?, która wywołała przemieszczenie punktu 1. Zgodnie z w^,cześniejszymi rozważaniami przemieszczenia w^r punktach 1 i 2 w odpowiednich kierunkach i wyw'ołane odpowiednimi silanu są sobie równe.

AlmaMater

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A.. Wdow^ka A.