82433

Część 2 7. METODA MIESZANA 2

Rozwiązanie powyższego układu znacznie uprości odpowiednie połączenie metody przemieszczeń z metodą sił. W metodzie mieszanej najkorzystniejszy będzie następujący układ podstawowy:

7^L

b

b

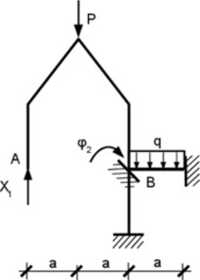
Rys. 7.3. Układ podstawowy ir metodzie mieszanej

W tak przyjętym schemacie statyczna zgodność z układem rzeczywistym zachowana została przez wprowadzenie siły X. ale zakłócona pizez wprowadzenie wewnętrznego utwierdzeniem. Kinematyczna zgodność została zakłócona odrzuceniem podpory w punkcie A

Układy podstawowy i rzeczywisty będą identyczne jeśli spełnimy następujące warunki:

M_b=0

Po icli rozpisaniu uzyskujemy układ równań kanonicznych

f 6_l,X_l+6,₃<p₃+A„=0 |r_;/ X,+r₃₃<p₃+ R_:f-0

W metodzie mieszanej ważna jest interpretacja niektórych w'spółczyruiików:

-    6_I3 jest przemieszczeniem pionowym punktu A wywołanym jednostkowym obrotem podpory B (o kąt

-    r₂, jest reakcją (momentem) w punkcie B wywołaną jednostkową silą przyłożoną w punkcie.4 (X = 1).

Kolejnym etapem jest wykonanie wykresów momentów w poszczególnych stanach.

AlmaMater

Dobra D.. Dztakirwlcz L.. Jainbroźrk S.. kanma M.. Mikołajczak E.. Przybylska P., Sytak A.. Wdowdca A