skanuj0016 (27)

Metoda analizy 'regresyjnej. '

■ -. • ■

. .    • Rozwiązując powyższy układ, zwany układem równań normalnych, otrzymuje

się szukane wartości b₀, b_lt..., b_K współczynników funkcji regresji o postaci (5.99). W przyjętym modelu matematycznym (5.99) obiektu sterowania założono częściową znajomość charakterystyki obiektu polegającą na znajomości postaci funkcji cp_k(u), k = 0,1,..., K. Założenie to tylko pozornie zmniejsza ogólność rozważań. W praktyce przyjmuje się bowiem funkcje <p_k(n) o postaciach:

(5.109)

; A- = bp+.buU_k + y] b_kki£-h 2 ^b‘J^l‘i^uj

u-1

KJ

(5.110)

Wn^1 •
• (p(lł) = uk	?r / II ►—* JO.	..,5 ^?
<p(jl) = w*	k * 1.2,.	..,,5
.>(«) = U,Uj	7= 1,2, .	.., S, lecz i < j

■"". 'A więc należy wyznaczyć na przykład charakterystykę obiektu (rys. 5.1) w postaci zależności;

Wprowadzimy obecnie dla obiektu nieliniowego formę zredukowaną funkcji . regresji, analogiczną do formy zredukowanej (5.84) w przypadku obiektu liniowego, w postaci ' .    . , ’ ' •

(5.111)

x_n—x = bu [<p3.(u„)-9?_a («)] + ...    («)-<?*(«)]

którą otrzymujemy w następujący sposób. Z pierwszego równania układu równań normalnych (5.106), po uwzględnieniu (5.101) otrzymujemy

(5.112)

X~ b₀+b₁(p₁(it)+b₂(p₂(ii)+ ... +b_K(p_K(u) przy czym: . .    :

•• V    N -    ■

(5.113)

t    * V .* '    1    , '^l :■    . .

N

1

. <pk(") = y

k= 1,2,..., K

(5.114)

-;Odejmując równanie (5.112) od równania (5.99) otrzymujemy formę zredukowaną (5.111). ^    , _:::_b '

’ Zadanie identyfikacji charakterystyki statycznej nieliniowego obiektu wielowymiarowego można również prosto przedstawić w zapisie macierzowym.

Poprzednio w celu ujednolicenia zapisu macierzowego funkcji regresji wpfo-wadziliśmy do macierzy sygnałów wejściowych (5.85) zmienną fikcyjną --    ■

_; ,. '_:i u_n0 = 1    . H = 1,2, ...,N    ’    (5.115)

, .‘Obecnie, podobnie, wprowadzimy funkcję    ■ ••

^: f dpoOO    ⁿ = 1,2, ...,N    ■    (5.116)

do macierzy danych wejściowych

>o("i)>    •••>    <Pk(j*0"

(5.117)

<Po(«2), 9>i(k2)».9»2(«2), •••> 9x(»₂)

_<Po(%)> 9>i(«*)» 9>2(«jv)» •••> 9fc(%)..

Funkcja regresji (5.99), przyjmie postać zgodnie ze wzorem (5.89) x—Ub    • ~    (5.118)

przy czym

*^r = (*„,*i.....&*)    ' •    . . _;    . . (5.119)

Kryterium minimalizacji (5.104) zachowa postać wzoru (5.90). Ostateczni rozwiązanie będzie mieć postać analogiczną do wzoru. (5.93)

-..b^ {U^TU)-'U^Tx ' y-    ; "•! a -: ‘-Z    (5.120)

z tym jednak zastrzeżeniem, że U jest określone wzorem- (5.117), a nie wzorem (5.85)., Zgodnie z uwagami, umieszczonymi po wzorze (5.93), macierz U^TU nic może być osobliwa, a więc kolumny macierzy U danych wejściowych (5.117) muszą być liniowo niezależne i liczba wierszy liniowo niezależnych powinna być nie mniejsza niż liczba K+l nieznanych współczynników b_k.

5.7. Ocena zgodności funkcji regresji z danymi doświadczalnymi

W poprzednich rozważaniach omówiono szczegółowo problem wyznaczania funkcji regresji. Znajomość funkcji regresji, charakteryzującej związek funkcyjny tkwiący w zależności statystycznej, umożliwia przewidywanie przeciętnego zachowania się obiektu. Dla dowolnego zestawu wartości wielkości wejściowych U_x> U₂, ..., U_s można obliczyć estymator wartości oczekiwanej wielkości wyjściowej X obiektu, będącej zmienną losową.

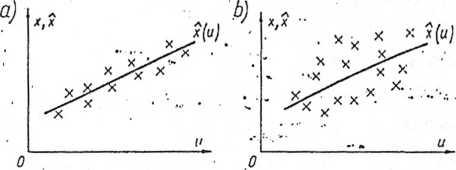
Rys. 5.5. Pole korelacji o różnym rozproszeniu

Znajomość funkcji regresji (5.99) nie umożliwia jednak, nawet bardzo ogólnie, oceny wartości rozbieżności między naszymi przewidywaniami a danymi doświadczalnymi. Jako przykład zostaną rozważone dwa pola korelacji przedstawione na rys. 5.5. Linie regresji w obu tych'przypadkach są opisane taką samą funkcją

x_n = x+b(u„—u)    (5.121)