skanuj0008 (44)

<j<0

Metoda analizy regresyjnej

Charakterystyka ta aprotćsymuje rzeczywistą charakterystykę obiektu (5:1), niewyznaczalną z powodu niemierzalności zakłóceń z_lt z₂,..., z_P w kolejnych chwilach n(n =1,2, ..., N)..

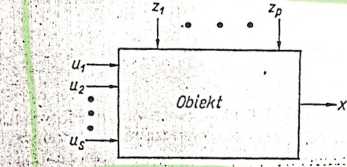
Rys Wielowymiarowy obiekt badany

i;.-;:-.f Aby' wyznaczyć optymalnie współczynniki b₀,b_1}...,' b_K naszego ..modelu -matematycznego (5^)_? należy przyjąć kryterium dobroci tego modelu, np. w postaci . funkcji-_; •

)jłjjy 'S_R-== S_R[{x_ly x₂, ...,x_N)}; {xi?Xii•••,xn}]    . . 'y \■ (5s4)T

określającej odległość [5.21] między zbiorami wartości wielkości wyjścipwych {¹i, x₂,Xh] obiektiT^Sd) i wyjściowych {x_ly x₂, •••, x_N) modelu&■&).

‘ . .W praktyce bardzo dogodnym kryterium jest po prostu odległość euklidesowa w przestrzeni N-wymiarowej, która sprowadza zadania wyznaczenia optymalnego zestawu współczynników b₀, b_ly..., b_K modelu (5.-3) do minimalizacji wyrażenia

' V .    ¹•    ..... ²

,    . w . .♦    u .    _____

' . ^sr -XI “ S    o> •••> W • '    (5'5)

. v    .«»/    ....... ...... • ■    ... ... ......■......

znanego od dawna w matematyce jako postulat lub zasada najmniejszej sumy kwadratów błędów.    ...    ... .    .    .    -    •

Zasada tą stanowi podstawę analizy rcgresyjnej. •.....•

..''I -ł-    ■ [rp\A^-<^    C,, di.    Ko -]k.

5.2. Zasada najmniejszej sumy kwadratów

. '. ,: ■*» '

•' ?    Zasada najmniejszej sumy kwadratów

Jeżeli jednak spróbujemy wyznaczyć współczynniki b₀ i b_y we wzorze (5.6), przyjmując jednocześnie u — u_n oraz x= x_n, przy czym n— 1,2.....9, to otrzymamy 9 równań    .    '

(5.7)

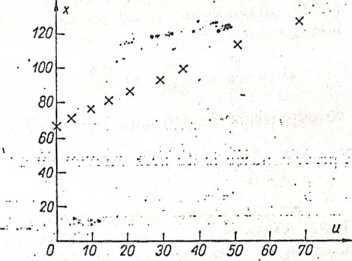
kYs. 5.2. Pomiary rozpuszczalności x azotanu sody \v.znlcżności od temperatury u

bo+bLUn n= 1,2,..., 9

Tablica 5.1

n	wn	^xn
1	0	66,1
2	4	71,0 •
3 '	1°	76,3 \
4	1'5 ^i:-^; :1'	^- 80,6
5 ■-	21	. 85,7
' • 6	.. ' .29 . ■ •	* 92,9:
7	36 '	99,4
8	51	113,6 ‘
9	68	125,1

o dwóch niewiadomych b₀ i b_t, przy czym równania te stanowią układ sprzeczny. Sprzeczność tych równań może być spowodowana bądź niedoskonałością teorii zakładającą zależność liniową, bądź błędami pomiarów, bądź łącznie jednym i drugim. Należy więc przyjąć związek (5.6) w postaci

(5.8)

(5.9)

x *= b₀-\-byii-\-c .== x+e przy czym e oznacza błąd, natomiast x = bo+byU • .•

jest aproksymacją^-rzeczywistego nieznanego związku. Podstawiając do wzoru (5.8) hasze obserwacje u„, x_n(n = 1,2,..., 9) otrzymujemy odpowiednik układu równań (5;7) w postaci 9 równań    ' •    •••>••>»-

’ . (5.10)

= b₀+bx u„+,e_n .. «:== l, 2, ..., 9

o 11 niewiadomych b_0f b_ly e_1} e₂,    Jest oczywiste, że nie można obliczyć

rzeczywistych wartości parametrów b₀ i byy bez względu na liczbę obserwacji N. Można-jedynie wyznaczyć pewne oceny'rzeczywistych‘wartości parametrów, które będą na ogół tym lepsze, im większa będzie liczba obserwacji N.

Należy znaleźć taki sposób wyznaczania wartości b₀ i b_{l y} aby wartości bezwzględne błędów e_n były łącznic małe. .    ...........

"■ Najprostszy pod względem rachunkowym okazał się postulat! najmniejszej sumy kwadratów błędów    '

(5.11)

Sr = 2 ^e" ^{= mIn}

1

Zasada najmniejszej sumy. kwadratów błędów [5.11, 5.20], zwana często zasadą najmniejszych kwadratów, została wprowadzona do matematyki przez Le-gendre’a (1806 r.) i Gaussa (1809 r.).    ’    ..•■•    ■ -    '■ •

2

Zasadę tę omówimy na klasycznym przykładzie [5.11] D. I. Mendelejewa z „Podstaw chemii” (1906 r.) dotyczącym rozpuszczalności x azotanu sodu w zależności od temperatury u.-Wyniki doświadczenia, zawierającego jY = 9 obserwacji,' podaje tabl. 5.1 oraz ilustruje.rys.'.5.2.j_r •._?:ovv^vv-^: '.' Na podstawie rozważań teoretycznych, bądź na'podstawie, analizy danych' doświadczalnych (rys. 5.1), można przyjąć zależność liniową rozpuszczalności a¹ od temperatury u w postaci    .    .    :• • •