89704

.leżeli B jest ustaloną bazą przestrzeni V, to odwzorowanie liniowe F : V —♦ W jest w zupełności wyznaczone przez swoje wartości przyjmowane na elementach bazy B, czyli układ F(B). Istotnie, dla każdego wektora v € V mamy przecież v = BMb(v), więc
Fv = F(BMb(v)) = (na mocy powyższej równości związanej z liniowością) = F(B)Mb(v).
Niech teraz C będzie dowolną bazą przestrzeni W. Biorąc Mc po obu stronach i korzystając ze wspomnianej już liniowości odwzorowania Mc, dostajemy
Mc(Fv) = Mc(F(B)Mb(v)) = Mc(F(B))Mb(v),
czyli
Mc(Fv) = Mc(F(B))Mb(v);
inaczej mówiąc,
jeżeli X = Mh(v), Y = Mc(Fv), to Y = AX. gdzie A = A/C(F(B)) = Xfg{F).
Inaczej mówiąc, kolumnę współrzędnych Y obrazu Fv dowolnego wektora u € V w ustalonej bazie C przestrzeni W otrzymujemy mnożąc kolumnę współrzędnych X tego wektora w bazie B przez ustaloną macierz A = MC(F(B)).
Z kolei, stosując powyższe stwierdzenie kolejno do poszczególnych wektorów u, bazy B = (vy, v2,... , vn) otrzymujemy, że kolejnymi kolumnami macierzy A są kolumny współrzędnych kolejnych wektorów Fi\ w bazie C, gdzie B = (tą,..., vn) (własność tę możemy stosować do wyznaczania tej macierzy). Macierz A = Mc(F(B)) nazywamy macierzą odwzorowania liniowego F przy ustalonej bazie B pierwszej przestrzeni (przestrzeni, na której odwzorowanie jest określone, dom F) i bazie C drugiej przestrzeni (w którą przekształca to przekształcenie, codom F) i oznaczamy przez M£(F). Tak więc M£(F) = Mc(F(B)).
W szczególnym przypadku, gdy V = W, tzn. gdy F jest operatorem liniowym, możemy (choć wcale nie musimy) wybrać C = B i mówić o macierzy operatora liniowego F w bazie B, czyli MH(F). Zauważmy także, że jeżeli V = W i F jest identycznością na V, to M§(id V) = Mc(B), czyli jest to omówiona już wcześniej macierz zmiany bazy.
Łatwo pokazać, że jeżeli przestrzenie wektorowe Vi.V2.V3 są skończenie wymiarowe, B, jest bazą V, (i = 1,2,3), zaś F : Vi —* V2 i G : V2 —+ Vz są odwzorowaniami liniowymi, to ich złożenie G o F = GF : V\ —* V3 (które, jak już wspomniano, jest również odwzorowaniem liniowym) w odpowiednich bazach ma macierz
M“'(GF) = M%(G)Mg(F).
Z powyższego wynika w szczególności, że odwzorowanie liniowe F : V —* W posiada odwzorowanie odwrotne G = F_1 : W —♦ V wtedy i tylko wtedy, gdy jego macierz Mq(F) jest macierzą odwracalną (a więc w szczególności kwadratową), i wtedy A/£(F-1) = [M^(F)]_I.
Pozostaje wyjaśnić, jak zmienia się macierz M%(F) przy zmianie bazy (w jednej lub w obu przestrzeniach), a w szczególności jak zmienia się macierz A///(F) przy zmianie bazy B. Oto odpowiednie wzory (F : V\ —* V2, Bi. B\ - bazy w V*, i = 1,2):
M%(F) = Mn.(B2) ■ A/g(F) • A/„,(Bi) = ■ M*(F) ■ Mb,(B\);
w szczególności gdy V\ — V2, By = B2 = B, B[ = B'2 = B1 mamy
M%(F) = AMB) • Mfj(F) ■ U„(B') = [A/«(B')]-' ■ M°(F) ■ AI„(B')
czyli
Mg(F) = N~l ■ Mg(F) ■ 1V
gdzie N = Mb(B') - macierz przejścia.
Zadania.
|
Xi |
\ | |
|
*2 | ||
|
53. | ||
|
.X\ |
/ |
2xt + x2 *2
1) Które z następujących przekształceń są liniowe?
: b) F : R2 - R. d) F : R2 -* F2,
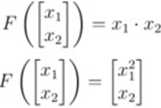
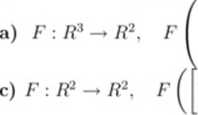
Wyszukiwarka
Podobne podstrony:
Jedyna ortonormalna baza przestrzeni (^2 to wektory e
Odwzorowania liniowe w przestrzeni wektorowejDefinicja 1. (odwzorowania liniowego) (X,K, +,-),(Y ,K,
10 (75) 226 10. Całkowanie form zewnętrznych gdzie B jest odwzorowaniem liniowym przestrzeni Rk w pr
16 3. Przestrzeń macierzy. Macierze odwzorowań liniowych (4) Jeżeli A e Mnn(K), to macierz B e Mnn(K
Ponieważ G jest bazą przestrzeni liniowej KG, współczynniki przy odpowiednich elementach grupy G mus
img1 (12) Co to jest baza danych? Słownik Webstera (http://www.m-w.com): baza danych to zbiór danych
page0079 75 jej części, tu i ówdzie rozproszone. Być rozciągiem w przestrzeni, to nie jest cecha dod
44 Jedyna ortogonalna baza przestrzeni [p2 to wektory e^ = (1)0),«2 = (0>1) • Punkty: OTrue x ®Fa
Image3 DODATKOWE 2005-01-12 3 Jest to relacja liniowego porządku, (d) Istnieje dok
Wyznaczanie współczynników reprezentacji Układ równań macierzowych v, v2 Vj-V jest bazą przestrzeni,
Pojęcie modela Klasyfikacja modeli. Model jest to odwzorowanie rzeczywistości lub jej fragmentu, jes
jedyna ortogonalna?za Jedyna ortogonalna baza przestrzeni [p2 to wektory e^ = (0,1
więcej podobnych podstron