2104510613
16
3. Przestrzeń macierzy. Macierze odwzorowań liniowych
(4) Jeżeli A e Mnn(K), to macierz B e Mnn(K) taką, że BA = I nazywamy macierzą odwrotną do macierzy A i oznaczamy A~l. Łatwo zauważyć (ćwiczenie!), że nie każda macierz (nawet różna od zera) ma macierz odwrotną.
Te i inne własności mnożenia macierzy wynikają natychmiast z interpretacji macierzy jako macierzy odwzorowań, o czym będzie mowa w następnej części.
3.2. Macierze odwzorowań.
BOISKO: Dwie przestrzenie wektorowe z bazami: (V,Bv), (W,Bw) i
odwzorowanie liniowe F: V —* W.
Niech e = (e\,... ,en) będzie bazą przestrzeni wektorowej V. Każdy wektor v € V ma jednoznaczną reprezentację v = X1ei + • ■ ■ + Xnen. Odwzorowanie
V
'A1'
_An_
jest izomorfizmem przestrzeni wektorowych. Kolumnę
-A1'
„ An_
oznaczać będziemy [v]Bv.
Niech / = (/i,... , fm) będzie bazą przestrzeni W i niech F : V —* W będzie odwzorowaniem liniowym. Mamy
F(v) = A1F(e1) + ■ ■ • + A nF(en)
+ A"[F(e„)]B'
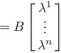
gdzie B = [6' j] i bj = [F(ej)]Bw. Wprowadzoną tak macierz B oznaczać będziemy [F]Bw B . Nazywamy ją macierzą odwzorowania liniowego F w bazach Bv i Bw-Ponieważ
r a1 -i
An
mamy
(3.1)
Wyszukiwarka
Podobne podstrony:
Rozdział 3. Przestrzeń macierzy. Macierze odwzorowań liniowych 3.1. Definicja i podstawowe
18 3. Przestrzeń macierzy. Macierze odwzorowań liniowych Przetłumaczmy na język macierzy uwagi na te
c) odwzorowania liniowe, macierz odwzorowania d) iloczyn skalamy
58 59 (14) 58Układy równań liniowych Jeżeli jeden z minorów stopnia 3 macierzy A jest niezerowy, to
Metody numeryczne - 2. Metody dokładne rozwiązywania układów równań liniowych Jeżeli macierz A dodat
16 2. Mapy i dane przestrzenne aby były użyteczne, ich parametry przestrzenne muszą być odwzorowanie
image 16 (2) Tam, w macierzystym lesie, Kędy wąsate wiją się porosty, Na podśoielisku miękkucbnych m
.leżeli B jest ustaloną bazą przestrzeni V, to odwzorowanie liniowe F : V —♦ W jest w zupełności wyz
10 (75) 226 10. Całkowanie form zewnętrznych gdzie B jest odwzorowaniem liniowym przestrzeni Rk w pr
12 2. Odwzorowania liniowe Dowód: (1) Jeżeli Wi,W2 6 F(V) to istnieją wektory Vi,V
Rozdział 2. Odwzorowania liniowe BOISKO: dwie przestrzenie wektorowe 2.1. Definicja i postawowe
Definicja: Jądrem odwzorowania liniowego h nazywamy podprzestrzeń h ‘({0}) przestrzeni E i oznaczamy
III IVa) Rys.7. Zapis różnych topologii danych przestrzennych: a) macierz blokowa M; b) składowe mac
3. MACIERZE I WYZNACZNIKI MATEMATYKA Definicja 3.16 Rządem macierzy A = [a1.a2,..., aTI] nazywamy ma
1.12 Napisać macierzowe równanie stanu układu liniowego f x(t) = Ax(t) + Bu(t), x(to) = xq y{t) =
więcej podobnych podstron