3818438387

Opisowe miary siły korelacji dwóch zmiennych

Siłę współzależności dwóch zmiennych można wyrazić liczbowo za pomocą wielu mierników. Ich wybór jest uzależniony m.in. od rodzaju cech, między którymi badana jest zależność (mierzalne, niemierzalne, mieszane); liczby obserwacji (tablica korelacyjna, szeregi korelacyjne), kształtu zależności (regresja, prostoliniowa, krzywoliniowa).

Zakładając, że współzależność badanych zmiennych losowych X i Y jest statystycznie istotna, możemy wyróżnić cztery rodzaje podstawowych miar sił korelacji tych zmiennych:

1.    współczynnik zbieżności Czuprowa;

2.    wskaźniki (stosunki) korelacyjne Pearsona;

3.    współczynnik korelacji liniowej Pearsona;

4.    współczynnik rang (korelacji kolejność i owej) Spearmana.

Współczynnik zbieżności Czuprowa

Miernik ten oparty jest na teście chi - kwadrat (y³). Wielkość £ jest podstawą do określenia unormowanej funkcji zależności cech zwanej współczynnikiem zbieżności Czuprowa. Określa go wzór:

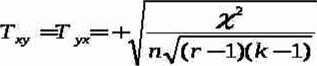
Współczynnik ten przyjmuje wartość z przedziału [0,1]-T=0, gdy badane zmienne są stochastycznie niezależne. Przy zależności funkcyjnej zmiennych, T = 0.

Im bardziej współczynnik zbieżności jest bliższy zeru, tym słabsza jest zależność między zmiennymi.

Przy wyznaczaniu współczynnika zbieżności nie jest ważne, którą z cech traktuje się jako zależną a którą jako niezależną - co jest istotne przy badaniu zależności w sensie korelacyjnym. Własność tę określa się mianem symetryczności:

T —T

*y    yx

Zaletą współczynnika zbieżności jest to, że może być stosowany do mierzenia współzależności zarówno cech mierzalnych jak i niemierzalnych, jego wadą jest natomiast to, że nie wskazuje kierunku korelacji (jest zawsze dodatni).

Do oceny natężenia korelacji między zmiennymi X i Y wykorzystuje się również współczynnik determinacji.

100-Tl

Miara ta wskazuje, w ilu procentach zmienność zmiennej zależnej jest określona zmiennością zmiennej niezależnej. Tak więc o ile z rachunkowego punktu widzenia T ocenia zarówno zależność cechy X od cechy Y jak i cechy Y od X , o tyle interpretacja współczynnika zbieżności musi jednoznacznie określać charakter zmiennych, tzn. która z nich jest zmienną zależną, a która niezależną.

Z uwagi na to, że przy obliczaniu współczynnika zbieżności brane są pod uwagę jedynie liczebności odpowiednich rozkładów, a nie ich parametry, współczynnik zależności jest przede wszystkim miarą zależności stochastycznej dwóch zmiennych. Ponieważ zależność korelacyjna jest pojęciem węższym od zależności stochastycznej można go wykorzystać jako miarę siły związku korelacyjnego.

Wskaźniki korelacyjne Pearsona