5020058887

Ćwiczenie 7

Badanie ruchu harmonicznego tłumionego

I. Zagadnienia do samodzielnego opracowania

1. Zasady dynamiki Newtona, energia kinetyczna i potencjalna.

2. Oscylator harmoniczny prosty.

3. Przykłady ruchu harmonicznego: wahadło matematyczne, fizyczne.

4. Drgania harmoniczne tłumione.

II. Wprowadzenie

Badanie ruchu harmonicznego tłumionego wykonujemy przy pomocy, tzw wahadła skrętnego, składającego się z krążka zawieszonego na stalowym drucie w ten sposób, że drut pokrywa się z osią obrotu krążka. Przymocowana wskazówka pozwala odczytywać kąt, o jaki obróci się wahadło. Zmianę współczynnika tłumienia drgań można regulować poprzez zmianę docisku trzech elementów hamujących umocowanych na płycie przyrządu.

Celem ćwiczenia jest wyznaczenie wielkości, które są charakterystyczne dla ruchu tłumionego, to jest częstości drgań tłumionych, logarytmicznego dekrementu tłumienia, współczynnika tłumienia.

III. Wykonanie ćwiczenia

1. Ustawić wahadło tak, aby wskazówka pokrywała się z zerem skali.

2. Wychylić wolno wskazówkę z położenia równowagi o kąt nie przekraczający

wartości —:

a. Odczytać wartość maksymalnego wychylenia (amplitudy) wskazówki po pewnym czasie t (np. po dwóch pełnych wahnięciach) a₀, a następnie wartość wychylenia a_n po czasie t + T. Jeżeli tłumienie jest małe i zmiana amplitudy jest niezauważalna po czasie t = T, zmierzyć amplitudę po czasie t = nT . Wtedy

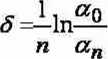
(1)

b. Wyznaczyć okres drgań F, mierząc czas ^ np. 5 wahnięć.

3. Zmienić wartość tłumienia poprzez regulację położenia elementów dociskowych.

4. Wykonać czynności opisane w punkcie 2 dla nowej wartości współczynnika tłumienia (3.

5. Obliczyć wartości okresu F, częstości drgań tłumionych co, korzystając ze wzoru (1) obliczyć logarytmiczny dekrement tłumienia i współczynnik tłumienia (3 .

6. Obliczyć oj_q korzystając ze wzoru

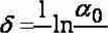
n a,

(2)

7. Wykreślić zależność kwadratu częstości drgań tłumionych oj w funkcji kwadratu współczynnika tłumienia f3 . Zależność ta powinna być liniowa (wzór (2)).