5020058889

Ćwiczenie 6

Pomiar siły Coriolisa

I. Zagadnienia do samodzielnego opracowania

1.    Kinematyka i dynamika punktu materialnego w inercjalnych układach odniesienia.

2.    Dynamika punktu materialnego w nieinercjalnych układach odniesienia.

3.    Zasada zachowania energii mechanicznej.

II. Wprowadzenie

Układ wirujący jest układem nieinercjalnym, w którym na znajdujące się w nim masy działają siły bezwładności. W ćwiczeniu kulka staczająca się z równi pochyłej trafia na środek obracającej się tarczy, po której dalej się porusza. A więc na kulkę będzie działać siła odśrodkowa i siła Coriolisa. Celem ćwiczenia jest wyznaczenie wartości przyśpieszenia i siły Coriolisa. Przyspieszenie Coriolisa wyraża się wzorem a_c =2®xv

gdzie: v - prędkość ciała,

a> - prędkość kątowa układu wirującego.

W omawianym układzie ruch kuli odbywa się w płaszczyźnie prostopadłej do osi obrotu układu wirującego, wektor a> jest zawsze prostopadły do wektora v i wartość przyśpieszenie Coriolisa możemy zapisać w postaci a_c = 2 va>

Istnieją dwa sposoby opisu zjawisk zachodzących w wirujących układach odniesienia (rys. laib):

-    opis z punktu widzenia obserwatora ruchomego (związanego z układem),

-    opis obserwatora nieruchomego względem układu.

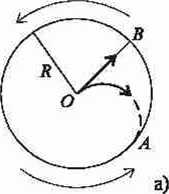
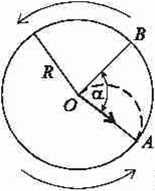
Rys. 1. Opis mchu ciała w układach wirujących: a) z punktu widzenia obserwatora ruchomego, b) z punktu widzenia obserwatora nieruchomego

Z punktu widzenia obserwatora ruchomego ruch ciała od punktu O do punktu A możemy rozpatrywać jako nałożenie się dwóch ruchów: ruchu jednostajnego wzdłuż prostej OB, w którym droga R wyraża się wzorem R = vt oraz ruchu jednostajnie przyśpieszonego po łuku BA. W tym drugim przypadku droga równa się długości łuku BA = ocR, lecz

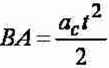
Porównując aR -

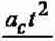
otrzymujemy:

2