3582308600

Ćwiczenie 8

Pomiar momentu bezwładności wahadła Maxwełla

I. Zagadnienia do samodzielnego opracowania

1.    Dynamika bryły sztywnej mchu postępowego i obrotowego - zasady dynamiki.

2.    Zasada zachowania energii.

3.    Wyliczanie momentów bezwładności ze wzoru całkowego.

II. Wprowadzenie

W mechanice klasycznej ważną rolę odgrywa zasada zachowania energii mechanicznej. Jeżeli na poruszające się ciało działają tylko siły zachowawcze, to całkowita energia ciała pozostaje stała i podczas mchu może nastąpić zmiana energii potencjalnej w kinetyczną i na odwrót.

Jako przykład można rozważyć tzw. wahadło (koło) Maxwella w postaci krążka zamocowanego na osi i zawieszonego bifilamie. Wahadło znajdujące się na pewnej wysokości h ma energię potencjalną:

Epot. =mgh

gdzie: m - masa krążka wraz z osią, g - przyśpieszenie ziemskie.

Uwolniony z podparcia krążek spada, wykonując ruch obrotowy i postępowy, a tym samym jego energia kinetyczna składa się z dwóch członów:

mv²

~Y~

W

2

- energia kinetyczna ruchu postępowego,

- energia kinetyczna ruchu obrotowego.

Zasada zachowania energii, przy zaniedbaniu oporów ruchu, wyraża się, więc równaniem:

mgh =

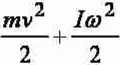
0)

gdzie: v - prędkość przesuwania się środka masy układu, r - promień krążka,

\

co- — prędkość kątowa w mchu obrotowym wokół osi krążka, r

1 - moment bezwładności krążka względem osi obrotu przechodzącej przez środek masy. Moment ten jest sumą momentu bezwładności osi wahadła, momentu

bezwładności samego krążka oraz dodatkowych pierścieni nakładanych na krążek w czasie wykonywania pomiarów.

Zakładając, że ruch środka masy krążka jest mchem jednostajnie przyśpieszonym, bez prędkości początkowej, to z równań

otrzymujemy związek:

2h v = — t

1