3582324947

Ćwiczenie 9

Sprawdzanie równania ruchu obrotowego brył I. Zagadnienia do samodzielnego opracowania

1.    Wielkości charakteryzujące kinematykę i dynamikę ruchu postępowego i obrotowego.

2.    Zasady dynamiki dla ruchu postępowego i obrotowego.

II. Wprowadzenie

W niniejszym ćwiczeniu posługujemy się wahadłem Oberbecka (rys. 1). Walec metalowy może obracać się wokół osi prostopadłej do osi przyrządu. Z walcem tym połączone są cztery pręty stalowe, na których nasadzone są walce. Położenie tych walców na prętach można dowolnie zmieniać. Na walcu osadzone są szpulki, na które nawija się nić. Na końcu nici przerzuconej przez bloczek zawiesza się ciężarki.

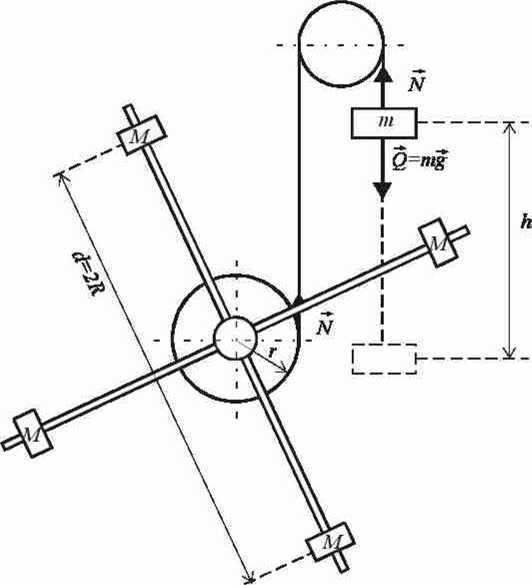
Rys. 1. Schemat wahadła Oberbecka

Na podstawie II zasady dynamiki możemy wypisać równania ruchu dla układu

rxN = Ie mg -N = ma

Zq względu na to, że wektory r i g są prostopadłe do osi obrotu, a wektor e jest do niej równoległy, możemy układ równań (1) zapisać w postaci skalarnej

N-r = Ie mg -N = ma

(2)