5020058904

Ćwiczenie 46

Wyznaczanie stałej siatki dyfrakcyjnej

I. Zagadnienia do samodzielnego opracowania

1.    Światło jako fala elektromagnetyczna.

2.    Interferencja fal świetlnych.

3.    Zjawisko dyfrakcji fal.

II. Wprowadzenie

Siatką dyfrakcyjną nazywamy zbiór dużej liczby równoległych wąskich szczelin, oddzielonych równymi, nieprzeźroczystymi przerwami. Siatkę dyfrakcyjną uzyskuje się np. przez zarysowanie równoległymi rowkami płask o-równoległej płytki szklanej. Powierzchnie nie zarysowane tworzą szczeliny, matowe rowki zaś nie przepuszczają światła. Odległość d równa sumie szerokości szczeliny i nieprzeźroczystej przerwy nazywa się stałą siatki.

Aby zrozumieć działanie siatki dyfrakcyjnej, zauważmy, że każda szczelina zgodnie z zasadą Huyghensa staje się źródłem fali cząstkowej. W ośrodku jednorodnym i izotropowym są to fale kuliste. Wskutek interferencji fal cząstkowych z każdej szczeliny wychodzą ugięte, rozbieżne wiązki światła.

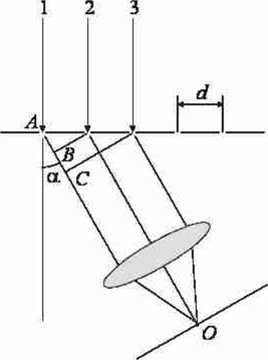
Rys. 1. Rozkład prążków dyfrakcyjnych na siatce dyfrakcyjnej

Rozpatrzmy wiązkę ugiętą pod kątem a . Różnica dróg między promieniami 1 i 2 czy 2 i 3 z sąsiednich szczelin wynosi AB = dsma, zaś między 1 i 3 - AC = 2c?sina, ogólnie między I i m + 1 promieniem - mdsm a. Jeżeli zatem promienie sąsiednie interferując dają maksimum, to wszystkie promienie sprowadzone do jednego punktu za pomocą soczewki wzmocnią się i dadzą silne maksimum.

Dla promieni ugiętych pod kątem a maksima otrzymuje się, gdy:

dńxuz = ki

Liczba k nazywa się rzędem widma. Przy tej samej wartości stałej siatki d, maksima powstają zawsze w tych samych miejscach, niezależnie od liczby szczelin w siatce. Maksima te nazywane są głównymi. Warunkiem powstawania maksimów jest, aby dla promieni sąsiednich różnica dróg równała się całkowitej wielokrotności długości fali 1. W siatce zawierającej m szczelin różnica dróg promieni skrajnych w tym przypadku wynosi mdsma = mkl. Im więcej szczelin w siatce, tym węższe i

l