6551262773

Matematyko Zbiór aodaó. Klmn i

Równanie ogólne prostej

3.38. Przedstaw równanie prostej k w postaci ogólnej:

3.39. Wyznacz równanie ogólne prostej k, do której naleią punkty A t 8, jeśli

a) 4(0,8), 6(2,4) c) 4( 3,2). 8(4,9)

b) 4(3. 4). 8(11, 4) d) 4( 2,6), 8(72, W2)

3.40. Wyznacz równanie ogólne prostej k przechodzącej przez dwa punkty p, q (skorzystaj bezpośrednio z równania ogólnego prostej), jeśli:

a) P(0, 4). Q(3,1) c) P{2, 2), Q(-l, 0)

b) ĄyfŚ, -3), Q(/5,8) d) P(3,1), Q( 1, -7)

3.41. Wyznacz równanie ogólne I kierunkowe (o ile istnieje) prostej * prostopadłe; do wektora u i przechodzącej przez punkt P, jeśli:

a) u= 1-1,2J,P(3,4) c) u‘-(5,0],P( 7,8)

b) v- f6, 1|, P(2, 5) d) u= (0, -3J, P(12, - 9)

3.42.    Wyznacz wartość parametru p, dla której proste k, I, m przecinają się w jed nym punkcie, jeśli: k: x * y +1 = 0, /: x ♦ p 0. m: 3x - y 9=0.

3.43.    Wyznacz wartość parametru m, dla której proste: k - prostopadła do wektora u *(2. 3) I przechodząca przez punkt P[ 1,6) orazp:x+y- 5 = 0

I n: x ♦ [m * 2)*y - 7 - 0 przecinają slą w jednym punkcie.

3.44.    Dla Jakiej wartości parametru m proste k: mx i- (m 1 4)y «i o orat k [m f l)x - my -10 = 0 przecinają się na osi odciętych?

3.45.    Dla jakiej wartości parametru m proste k:x my-tmi 4-0 oraz 1:2mx * y m 1*0 przecinają się na osi rzędnych?

c) ♦ y » 1 . o

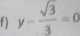
3.46.    Podaj miarę kąta. jaki tworzy z osią OX prosta dana równaniem ogólnym

•) X4 y 7*0    b) &X-y+ 90 0

d) s/3* 3y * 15-0 e) x S-0