2277150846

co pokazuje poniższy rysunek. Występujący w pierwszym z powyższych równań czynnik 2A₁A₂cos{(p₂ — <Pi) nazywamy wyrazem interferencyjnym, który podkreśla istotę stałości faz.

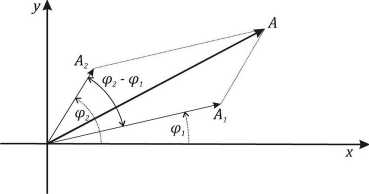
Rys. 1.5. Interferencja dwóch fal o jednakowych częstościach, ale różnych fazach i amplitudach.

Wyprowadzone powyżej relacje wynikają także z relacji geometrycznych.

Efekt Dopplera

Ciekawe zjawisko obserwujemy w sytuacji, gdy obserwator porusza się względem źródła emitującego fale. Wówczas częstotliwość sygnału emitowanego przez źródło jest inna od częstotliwości rejestrowanej przez obserwatora. Dla fal rozprzestrzeniających się w ośrodku, takich jak na przykład fale dźwiękowe, efekt zależy od prędkości obserwatora oraz źródła względem ośrodka, w którym te fale się rozchodzą. W przypadku fal rozchodzących się bez udziału ośrodka materialnego, jak na przykład światło w próżni (w ogólności fale elektromagnetyczne), znaczenie ma jedynie różnica prędkości źródła oraz obserwatora.

Rozważmy prostą sytuację przedstawioną na rysunku 5 gdzie zarówno źródło Z jak obserwator O poruszają się wzdłuż prostej w tym samym kierunku, znaczmy prędkość obserwatora przez V, prędkość źródła u, natomiast prędkość emitowanego zaburzenia w danym ośrodku jako c.

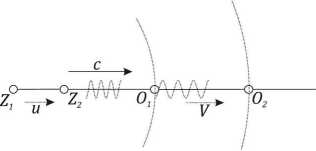
Rys. 1.6 Efekt Dopplera

18