3262347656

q_vr = div[sE + P_r) = divD

(2.5)

(2.6)

Należy podkreślić w tym miejscu, że ładunek polaryzacyjny q_yp nie należy utożsamiać z polaryzacją natychmiastową, którą łatwo określić z zależności P, = SoXE, gdzie x jest podatnością elektryczną a jako ładunek polaryzacyjny wynikający z trwałej zamrożonej polaryzacji Zaistnieje wiele metod badania rozkładu ładunku elektrycznego, zasadniczo polegają one na analizie zaburzeń cieplnych lub mechanicznych w badanej próbce [40, 23], Wspólnym mianownikiem metod badawczych rozkładu ładunku jest czasowe, nieniszczące przemieszczenie ładunku przestrzennego wywołane lokalnym zaburzeniem wędrującym przez próbkę. W obwodzie zewnętrznym objawia się to zmianą gęstości prądu

7(0 =

dD(zJ)

dt

(2.7)

(2.8)

Po podstawieniu do równania podstawowe równanie materiałowe D(z,t) = e₀s_rE(z, t) + P_r(z,t)

rozwiązanie równania daje zależność na prąd zwarcia próbki (napięcie na próbce równe zero)

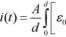
^-^E^z, t) + s₍₎e_r dt    ^{0 r}

dE(z,t) dP_r(z,t) dt    dt

(2.9)

gdzie A pole powierzchni elektrody pomiarowej a d grubość próbki. W przypadku pobudzenia termicznego (dT/dt) obserwowany prąd zwarcia próbki można wyrazić w postaci:

...    A rl"    de_r    ,    dE(z,t) dP_t(z,t)~\dT .    _1A.

^,('^{) =} rffr°sr^£(z''^)+v'^7^⁺^F-k    ⁽²¹⁰⁾

natomiast w przypadku ekscytacji za pomocą fali ciśnienia (dS/dt)

...    A",\    de_rr,,    ,    3E(z,t) dPXz,t)^8S ,

u