3754969710

15

2.3. GEODEZYJNE

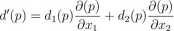
Aby policzyć iloczyn skalarny (wyznaczony przez metrykę Riemanna) wystarczy policzyć:

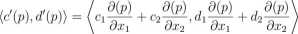
2

— gncidi + g\2C\d2 + <72102^1 -f <72202^2 — ^ gijCidj

i,j=l

Wobec tego iloczyn skalarny wyznaczony przez metrykę Riemanna odpowiada formie dwuliniowej o macierzy [gij\i,j=i,2-

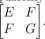
Definicja 2.2.6 (pierwsza forma kwadratowa). Macierz [gij] zdefiniowana powyżej wyznacza formę kwadratową, którą bedziemv nazywać pierwszą formą kwadratową.

Tradycyjnie jej macierz oznacza się:

Określenie metryki Riemanna, pozwala nam zdefiniować długość krzywej na powierzchni. Niech c: [a, b] —> U C M będzie dowolną krzywą różniczkowalną, wtedy długość tej krzywej wynosi:

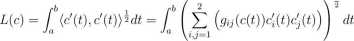
2.3 Geodezyjne

Definicja 2.3.1 (geodezyjna). Niech c: I —> M będzie parametryzacją krzywej, proporcjonalną do długości. Jeśli dla każdego to € I istnieje S > 0 taka, że każdy odcinek cl^^j długości mniejszej niż S jest najkrótszą krzywą łączącą c(£o) z c(£i), to mówimy, że c jest krzywą geodezyjną.

Przykład 2.3.2. Rozważmy sferę dwuwymiarową w R³. Pomiędzy dwoma punktami leżącymi na antypodach możemy poprowadzić nieskończenie wiele geodezyjnych. Jeśli natomiast wybierzemy dwa punkty leżące na równiku to istnieje dokładnie jedna geodezyjna łącząca te punkty.

Przykład 2.3.3. W przestrzeni R² geodezyjne to odcinki.

Twierdzenie 2.3.4. Niech M będzie powierzchnią, wówczas:

(i) dla każdego p G M i v G T_PM istnieje e > 0 i dokładnie jedna, sparametryzo-wana łukowo geodezyjna c: (—e, e) —> M taka, że c(0) = p i c'(0) = v;

(ii) dwa dowolne, dostatecznie bliskie punkty M można połączyć dokładnie jedną, sparametryzowaną łukowo geodezyjną.