3813573812

gdzie: @ to kąt pomiędzy wektorami.

Jeśli znamy współrzędne wektora w płaskim układzie kartezjańskim:

A = a_x e_x + a_y e_y \ B = be_x + b_y e_y

iloczyn skalarny możemy policzyć w następujący:    A ■ B = a_x • b_x + a_y ■ b_y

•    Iloczyn skalarny jest przemienny: A .B ₌B • A

•    Jeśli zapiszemy iloczyn skalarny w następującej postaci:    >1 • 5 — [>T| • cos 0 [b|

to możemy zauważyć, iż P*|' ^COs ® jest długością rzutu wektora A _na wektor B.

•    Jeśli wektory są równoległe, iloczyn skalarny osiąga maksymalną wartość/* ’ ® ⁼ |^| ’ |^|' ^COs ® ⁼ 1^1' l®l

• Jeśli wektory są prostopadłe, iloczyn skalarny jest równy 0:    >1 • 5 = |^4| -1^| • cos 90 = 0

•    W płaskim układzie kartezjańskim iloczyn skalarny wynosi: A ■ B = a_x ■ b_x + a_y ■ b_y

Zadanie 7.

Dane są dwa wektory: A = [3,3i/3], B = [3, V3]. Oblicz ich iloczyn skarlany dwoma poznanymi przez ciebie sposobami.

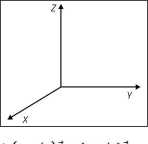
Trójwymiarowy układ współrzędnych kartezjańskich.

W przestrzeni trójwymiarowej przyjęto konwencję stosowania różnych układów współrzędnych, między innymi kartezjańskiego, pokazanego na rysunku obok. Wektory są w nich wyrażone za pomocą trzech liczb,

(współrzędnych) określających stosunek długości rzutów wektora na odpowiednie osie do długości wersorów osi:

A = (a_x a_y a.), B = (b_x b_y b_z) lub A = a_x e_x + a_y e_y + a_se_z j B = b e_x + b_y e_y + b_z e_z Analogicznie, suma:

C = A + B = a_x e_x + a_y e_y + a_ze_z + b + b_y e_y + b_z e_z = (a_x + b_x) e_x czy tez iloczyn skalamy: A ■ B = a_x ■ b_x + a_y ■ b_y + a_z ■ b_z

Iloczyn wektorowy.

Iloczyn wektorowy wektorów A i B oznaczamy w następujący sposób: C = A x B Wynikiem mnożenia wektorowego dwóch wektorów jest wektor C, którego:

• długość jest równa: FbPI-FI- sin(^), gdzie <t> jest mniejszym z kątów pomiędzy wektorami A j B,

•    kierunek jest zawsze prostopadły do płaszczyzny wyznaczonej przez wektory A i B,

•    zwrot określony jest tak, aby układ tworzony przez wektory A, B i C był układem prawoskrętnym Innym sposobem znalezienia iloczynu wektorowego jest obliczenie wyznacznika:

Ć = AxB = a_x a_v a₇ = {a_yb. -b_ya, )e, + {b_xa_z -a_xb.)e_y + (a_xb_y -b_xa_y )e.