4736386896

ROZWIĄZANIE ZADANIA 11

Rozwiązujemy nierówność: x² - 3nx + 2n¹ < 0.

„ . . _ ₂ „ ₂    2    3n-n    3« + m „

Stąd A = 9« - 8» = « , x. =-= n. x, =-= 2w .

2 ² 2

Stąd x e (/?, 2n ), gdzie neN a n > 1.

Największą liczbą całkowitą spełniającą nierówność jest x = 2n -1. Zatem szukana funkcja jest postaci:

/(«) = 2n - 1.

ROZWIĄZANIE ZADANIA 12

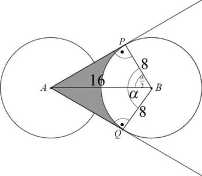
Pole wycinka jest równe: _c cr_D2    a 8    \ a

uffinka ₂    S    2    16    2    2

Zatem

Pole zacieniowanej figury ó’,, równa się:

S_F=S_a-S_wycinka

gdzie S„=2-S'_ABD.

Wykorzystując twierdzenie Pitagorasa Obliczamy długość boku AP trójkąta prostokątnego ABP:

\AP\‘ =16² - 8² =192, zatem |^/>| = 8^. Pole czworokąta równe jest:

S_a = 2-y 8-8>/3 =64^.

n

7'

Pole szukanej figury:

S_r = 64n/3 -yir = 64^ -© Centrum Kształcenia Akademickiego „CK.A ", Gliwice 2006.

Pełne rozwiązania zadań opracował zespół Centrum Kształcenia Akademickiego CKA. Nie są to oficjalne rozwiązania prezentowane przez Centralną Komisję Egzaminacyjną. Nieautoryzowane rozpowszechnianie całości lub fragmentów rozwiązań zadań w jakiejkolwiek postaci jest zabronione bez zgody CKA. Wykonywanie kopii metodą kserograficzną, fotograficzną a także kopiowanie na nośniku filmowym, magnetycznym lub innym powoduje naruszenie praw autorskich niniejszej publikacji.

strona 13

© CKA 2006. Plik pobrany ze strony www.zadania.pl - Matematyka - rozwiązania zadań Arkusz II