4806164934
2.1 Zależność między wychyleniem, prędkością i przyspieszeniem 2 DRGANIA HARMONICZNE PROSTE
Prędkość obiektu wynosi wtedy
—Aui sin(wt + 4>)
a przyspieszenie
*=$=i (S)=i +«)=+« = -“2-
Z ostatniego równania wynika, że w ruchu harmonicznym musi być spełniona zależność
d?x _ 2
d? ~ *
Jeżeli drgający obiekt jest materialny to po pomnożeniu obu stron przez masę drgającego ciała (2.2) przyjmie postać
d?x m dt2
F
Tak więc aby ciało drgało harmonicznie, siła działająca na nie musi być proporcjonalna do wychylenia lecz przeciwnie do niego (wychylenia) skierowana.
Rysunek poniżej przedstawia porównanie czasowego przebiegu wychylenia, prędkości i przyspieszenia ciała drgającego ruchem harmonicznym prostym
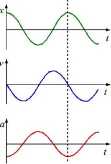
Rysunek 2: Porównanie czasowego przebiegu wychylenia, prędkości i przyspieszenia dla ciała drgającego ruchem harmonicznym prostym. Zauważ, że wykresy są względem siebie przesunięte!

©Mariusz Krasiński 2006
Wyszukiwarka
Podobne podstrony:
DSC02967 (2) 1.1.1. Drgania harmoniczne _.....(sinusoidalne) e / Prędkość / Przyspieszenie Rys. 1.1.
HPIM0608 Drgania harmoniczne - siła proporcjonalna do wychylenia i skierowana do punktu równowagi
skanowanie0056 (2) - Zależności między przyspieszeniami liniowymi alta2, a3 a’przyspieszeniem kątowy
75992 s gli7 Zależność między średnicą ziaren a prędkościami prądu wody, przy których następuje eroz
Ruch harmoniczny (2 godz) Droga w ruchu harmonicznym, prędkość, przyspieszenie, siła. Graficzna
3 19. zna i stosuje w zadaniach zależność między prędkością liniową i kątową 20.
Zdjęcie338 (3) Zależności między osiąganym współczynnikiem wzmocnienia siły i prędkości a liczbą
2. Otrzymać zależność między momentem pędu i prędkością kątową obracającej się wokół stałej osi
27937 skanuj0397 drgania, i równe zeru dla tych punktów (a = 0), z których wydaje się, że ładunek ni
arcz 112 o V, h V[km/h Rys. 7.2. Zależność między prędkością obrotową silnika a prędkos cią jazdy Pr
skanuj0038 (78) xyo xyo Rys. 1.23. Zależności między współrzędnymi atomów wodoru w
więcej podobnych podstron