490575240

2

ROZDZIAŁ 1. GRUPY

kwadratowych stopnia n o elementach z ciała F. Specjalna grupa liniowa SL(n, F) składa się z wszystkich macierzy kwadratowych stopnia n o elementach z ciała F, których wyznacznik jest równy 1.

(d) Grupa kwatemionów Quat. W grupie SL(2, C) weźmy macierze

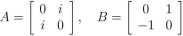
Wtedy A⁴ = B⁴ = I, A² = B², BAB ¹ = A ¹ i równości te pozwalają stwierdzić, że następujących 8 macierzy

/, A, A², A³, B, AB, A²B, A³B

tworzy grupę. Nazywamy ją grupą kwatemionów i oznaczamy Quat lub Q.

(e) Grupa diedralna D(n). W grupie permutacji S(n) weźmy permutacje

*⁼⁽ⁱ²-'-ⁿ⁾’    »=(« Ti—i::: ")•

Sprawdzamy, że xⁿ = y² = 1, yxy~¹ = x~^l. Równości te pozwalają stwierdzić, że 2n permutacji

l,x,... ,xⁿ~¹,y, xy,... ,x^1l~¹y

tworzy grupę. Nazywamy ją grupą diedralną i oznaczamy D(n) (lub D_n). Grupę tę nazywa się także grupą izometrii n—kąta foremnego, gdyż numerując wierzchołki n—kąta foremnego liczbami 1,2,... ,n stwierdzamy, że x i y, a także każdy element grupy D(n), można zinterpretować jako izometrię tego n—kąta. Faktycznie są to wszystkie izometrie n—kąta foremnego.

Obszerną listę przykładów można znaleźć w [S], zad. 001 020.

1.1.2 Podgrupy i warstwy

Podgrupą H grupy G nazywamy podzbiór grupy G zamknięty ze względu na działanie grupowe (jeśli a,b € H, to także ab € H), który sam jest grupą ze względu na działanie będące zacieśnieniem działania na G do H. Piszemy wtedy H < G.

H < G wtedy i tylko wtedy, gdy spełniony jest warunek:

x,y € H => xy~^x € H.

Łatwo stwierdzić, że część wspólna dowolnej rodziny podgrup grupy G jest podgrupą grupy G. W szczególności, jeśli A jest podzbiorem grupy G, to część wspólna wszystkich podgrup grupy G zawierających zbiór A jest podgrupą grupy G. Nazywamy ją podgrupą generowaną przez zbiór A i oznaczamy (A). Na przykład, grupa kwatemionów Quat jest podgrupą grupy SL(2, C) generowaną przez macierze A, B z przykładu l.l.l(d). Podobnie, grupa diedralna D(n) jest podgrupą S(n) generowaną przez permutacje x, y z przykładu l.l.l(e), zatem w grupie S(n) mamy (x,y) = D(n).

Dla podzbiorów A i B grupy G określamy ich iloczyn kompleksowy A ■ B := {a ■ b e G : a € A,b e B}.