8416073537

wartości zespolone. Z uwagi na tę tożsamość, wszystkie metody opracowane dla liniowych obwodów prądu stałego znajdują zastosowanie dla liniowych obwodów prądu sinusoidalnego analizowanych z zastosowaniem metody symbolicznej.

W metodzie symbolicznej „przepisy” na układanie równań Oczkowych i równań węzłowych, na wartości parametrów gałęzi równoważnych, na transfigurację gwiazda-trójkąt (i odwrotnie), są identyczne jak dla prądu stałego, przy czym zamiast rezystancji i konduktancji występują impedancje i admitancje zespolone, a zamiast napięć, prądów oraz sił elektromotorycznych i prądomotorycznych - ich wartości skuteczne zespolone. Stąd metody te nie będą już ponownie wyprowadzane lub uzasadniane, zostaną jedynie pokazane w przykładowych zastosowaniach.

9.1.    Obliczanie obwodów metodą układania równań z praw Kirchhoffa

1Q    1 mF 1Q

Zapoznawanie się z metodami analizowania obwodów prądu sinusoidalnie zmiennego zaczniemy od metody układania równań z praw Kirchhoffa. Jest to metoda podstawowa - o nią oparte są wszystkie inne.

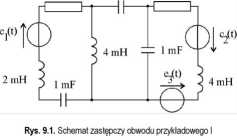
Rozważmy obwód przykładowy I o schemacie zastępczym przedstawionym na rys. 9.1. Należy dla niego wyznaczyć przebiegi wartości chwilowych wszystkich prądów.

Dane nie podane na rysunku:

e,(Q = 4 sinf500-t-—)V,

^e2(t) =8y[2cos(500-t)V,

e_3(l)=2j2sm(500-t)V

Zastosujmy do tego zadania metodę symboliczną. W tym celu wyznaczmy impedancje zespolone wszystkich elementów oraz wartości skuteczne zespolone wszystkich występujących w obwodzie sił elektromotorycznych.

Pulsacja ma wartość: co = 500

s

Stąd wartości impedancji:

Z_c=-j — = -j---_T = -j2n; Z,, = j<oLi = i 100-1-W³ = j0,5 22,

®^c 500-l-10~³

z_u = jmL₂ = j 500-4-10'³ = j2n

Wartości skuteczne zespolone SEM:

. TC    .K

Ej=^=e ⁴ = (2-j2)V, E₂=*e 2_=j8V, E₃ = 2eJ°=2V \2

Schemat zastępczy obwodu z danymi do stosowania metody symbolicznej przedstawia rys.

9.2.    Przy poszczególnych elementach pasywnych podano wartości ich reaktancji lub rezystancji, a nie impedancje zespolone. Można tak zrobić gdyż zastosowane na schemacie symbole jednoznacznie wskazują, które z tych elementów są idealnymi kondensatorami, które idealnymi induktorami, a które idealnymi rezystorami, zatem określenie wartości ich impedancji zespolonych nie stwarza żadnych trudności. Gdyby w schemacie zastępczym występowało źródło