8955899117

172

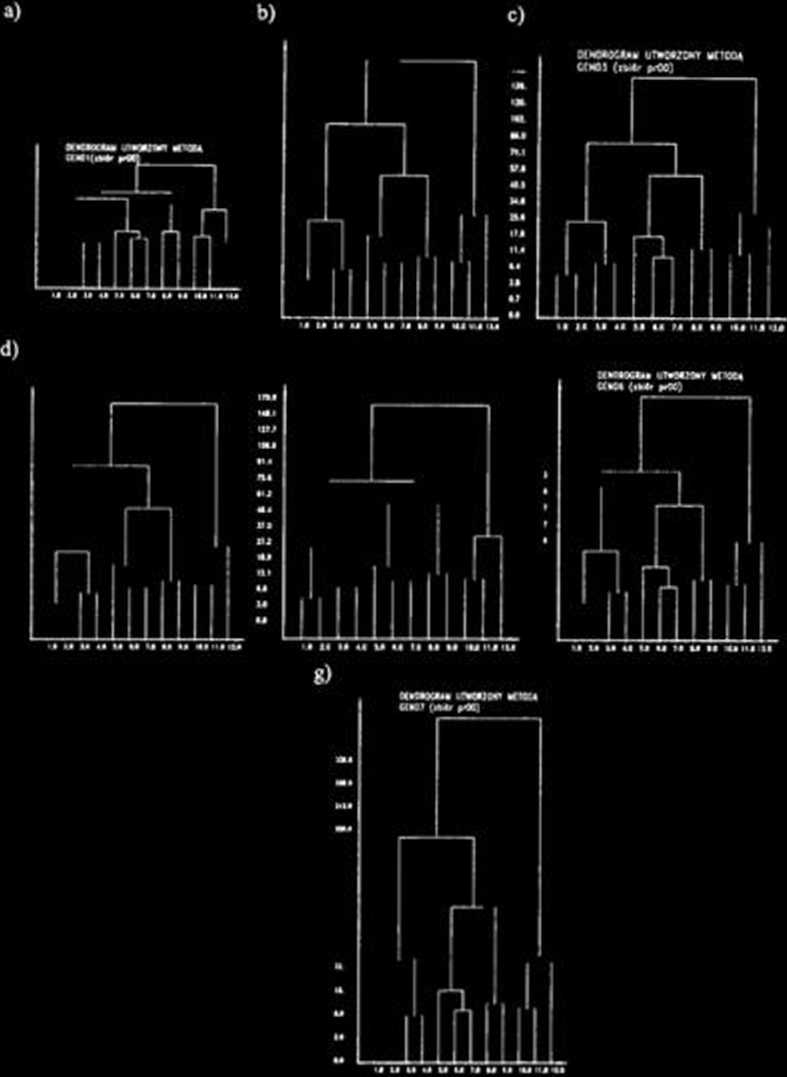
Ryj. 5.8.15. Dendrogramy hierarchicznej klasyfikacji utworzone metodą GEND 1 - 7 Fig. 5.8.15. Dendrograms of hierarchical classification created using the method GEND 1-7

W programie GEN 323 generowany jest również zapis układów klas UH* {A*......A*} dla

N»2-(M-1) w formie pliku (RK kia), tabl. 5.8.6, które stanowią wstępny układ klas dla klasyfikacji iteracyjnej.

Tablica 5.8.6

Zapis układów klas dla N-2-(M-l)

| Nr konstrukcji

□

□

□

□

□

□

□

□

□

EE

m

E

UKiad Klas U(N) dla N-

□

a

□

□

□

a

□

□

□

□

□

□

□

a

D

□

a

□

□

□

□

□

□

□

□

□

□

D

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

a

□

a

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

□

a

□

□

□

□

□

□

□

□

□

□

□

□

n

□

□

□

□

□

□

□

□

□

□

□

□

D

a

D

□

□

□

□

□

□

□

□

E3

□

5.8.3.2. Klasyfikacja itcracyjna

Liczba możliwych układów klas dla znanej liczby klasyfikowanych konstrukcji iz (ks"‘(m = i). gdzie: i=l, izjoraz założonej liczby klas N jest określona w publikacji (12. 161] zależnością:

K«z.N) = -l£(-l)'| ^NWr)- .    (5.96)

N r-C ¹    1

Dla liczby klasyfikowanych konstrukcji iz-15 oraz liczby klas A'“5 możliwych jest 2.734*10⁹ układów klas Aby z tak licznego zbioru możliwych układów klas osiągnąć optymalny -kład klas. konieczne jest postępowanie metodyczne. Metodą pozwalającą utworzyć optymalny układ klas spełniający krytena KK1 i KK2 jest metoda itcracyjnej klasyfikacji (54] Polega ona na iteracyjnym udoskonalaniu wstępnego układu klas U* o założonej liczbie klas .V tak. aby sumaryczne rozproszenie klas było minimalne:

H(U⁰n)>H(U^,n)>H(U^,)>......H(UŁ)-H(U*_n).    (5.97)

Pierwsze stadium klasyfikacji itcracyjnej dla zadanej liczby klas N nazwano klasyfikacji prostą Opracowano następujące stadia klasyfikacji prostq:

1)    dla każdej konstrukcji k, sprawdza się, czy jej przemieszczenie z klasy A,^N do jednej z pozostałych klas A^N powoduje spełnienie nierówności:

-    - (5 98)

(dla n,*l nie jest realizowane przemieszczenie konstrukcji k, z klasy A* do klasy A^N).

2)    jeżeli spełniona jest powyższa nierówność, to konstrukcja k, jest przenoszona do nowej klasy i obliczane są ponownie miary oceny układu klas,

3)    proces itcracyjny trwa tak długo, aż żadne przeniesienie konstrukcji nie zmniejszy sumarycznego rozproszenia klas H(U(,),

4)    dla tak wyznaczonego układu klas oblicza się następnie sumaryczne odseparowanie między klasami D(Un).