9739661618

wykres mocy i oś odciętych (oś „iksów”) jest równe podobnemu polu z ćwiartki pierwszej. Tym razem jest ono proporcjonalne do ilości energii jaka z cewki odpłynęła. Całą energię, którą cewka pobrała w pierwszej ćwiartce okresu w drugiej ćwiartcei oddaje. W ćwiartkach trzeciej i czwartej okresu te procesy energetyczne powtarzają się (z odwrotnym zwrotem prądu i pola magnetycznego).

Zatem idealna cewka indukcyjna „średnio” nie pobiera żadnej energii. Obliczana za okres wartość średnia jej mocy, a więc moc czynna jest równa zeru:

_ 2n

Pl = pi =--\U ii-sinflcot + 2\f/j )dcot = 0

²ⁿ o

Cewka nie pobiera takiej energii, która przepływ byłby jednokierunkowy, która zamieniana byłaby bezpowrotnie na energię nieelektryczną. Zjawiska energetyczne jakie w niej zachodzą polegają wyłącznie na oscylacyjnym przepływie energii pomiędzy odbiornikiem i źródłem. Występowanie takich oscylacji interpretowane są w elektrotechnice jako występowanie mocy biernej (por. pkt. 6.3. rozdz.6.). W przypadku cewki moc ta nosi nazwę mocy biernej indukcyjnej - Q_L

Definiuje się jąjako iloczyn wartości skutecznych prądu i napięcia cewki:

Ql=U_l1    (7.14)

Jak widać z wzoru (7.13) jest to jednocześnie amplituda oscylacji mocy cewki, co bywa traktowane jako fizyczna interpretacja mocy biernej indukcyjnej.

Podstawiając do wzoru (7.14) wzór (7.9a) otrzymujemy jeszcze inny wzór na obliczanie mocy biernej indukcyjnej.

Ql=*_LI²    (7.14a)

Jednostką mocy biernej indukcyjnej nie jest wat jak dla „zwykłej”, „prawdziwej” mocy. Aby podkreślić, że to nie jest ta „prawdziwa” moc, wprowadzono tu nową jednostkę - var (czyt.: war). Jest to skrót od „Volt-Amper-reaktancyjny”.

\[Q_L] = [u]-[i] = lVA = \var

Niekiedy stosuje się zapis: var_jn(j.

Współczynnik mocy cewki indukcyjnej jest równy zeru (A/, = — = —= 0).

^SL Ul¹

element zachowawczy

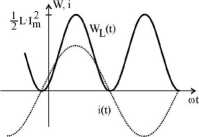
Rys. 7.14. Przebieg czasowy energii induktora idealnego

Cewka indukcyjna klasyfikowana jest jako magazynowana (zachowywana) jest w jej polu magnetycznym i może być z powrotem zamieniona na energię elektryczną. Inna nazwa elementu zachowawczego to element reaktancyjny (taki, który charakteryzowany jest przez reaktancję).

Przebieg czasowy wartości energii zgromadzonej w danej chwili czasowej w polu magnetycznym induktora określa zależność:

W_L(t) = ii/²(t) = jL■ ll ■ sin²(s>l +    )

Przebieg ten, na tle przebiegu czasowego prądu pokazano na rys. 7.14.

7.3. Kondensator idealny

Kondensator to układ dwu przewodników przedzielonych materiałem nieprzewodzącym (dielektrykiem, także próżnią). Taki układ może być zbudowany celowo, może też powstać w