1053228392

— 298 —

a un ensemble parfait F fixe, donnę comme noyau, un ensemble jouissant de la meme propriete.

En effet, soit {E^ ^ le systeme determinant en question et E son noyau.

II existe un systeme    compose d'ensembles (F_z)

• §

et tel que:

F    = F

i\.    k Z' ^łl

pour chaque cortege d'indices. Soit E' le noyau du second systeme determinant. On a:

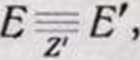
donc il y existe deux ensembles p et q de l^re cetegorie par rapport a F et tels que

E = E' — p + q.

L/ensemble E^r c'est un ensemble (A) comme le noyau d'un systeme determinant d'ensembles du type (F_z). D'apres le the-oreme de M. M. Lu sin et Sierpiński E' satisfait a la condi-tion de Baire. Par consequant E y satisfait aussi.

Pour des ensembles mesurables le raisonnement est analogue