1484605990

3. Algorytm HITS

HITS (Hyperlink Induced Topie Search) łączy ocenę istotności na podstawie zawartości strony z rankingiem opartym na strukturze połączeń (często połączenia nie mają nic wspólnego z popularnością; najbardziej popularne strony nie muszą być odpowiedziami na zapytanie).

Pomysł: skupienie się na istotnych stronach i obliczenie ich popularności z uwzględnieniem podziału na dwie

grupy:

■    autorytet (authorities) jest wskazywany przez wiele koncentratorów - tu można znaleźć istotną informację,

■    koncentrator (hubs) wskazuje na wiele autorytetów - mówi gdzie można znaleźć informację.

HITS działa na zależnej od zapytania części grafu sieci (IBM website vs. Computer hardware). Zaczyna od przeszukiwania według słów kluczowych, a potem analizuje strukturę połączeń dla otrzymanych istotnych stron (wydobywanie tematu):

■    znajdź za pomocą standardowego systemu wyszukiwania informacji tekstowych (niewielki) zbiór istotnych stron internetowych nazywany zbiorem-korzeniem R„ (root set);

■    rozszerz zbiór-korzeń przez dodanie stron, które cytują i są cytowane przez strony ze zbioru-korzenia; powstaje zbiór bazowy S_q (base set) (dobry autorytet może nie zawierać słowa kluczowego, ale znajdzie się w zbiorze bazowym, jeśli koncentrator był częścią odpowiedzi na zapytanie i vice versa; czyli zbiór koncentratorów i autorytetów w analizowanej puli jest wzbogacony);

■    przeanalizuj strukturę połączeń w S_q, aby znaleźć autorytety i koncentratory:

■    niech L będzie macierzą sąsiedztwa grafu, gdzie L(i,j)=1 jeżeli strona i cytuje stronę j, a L(i,j)=0 w przeciwnym razie (i oraz j należą do Sq);

■    niech a = (ai a₂.... a„) będzie wektorem autorytetu, h = (h_t h₂.... h„) wektorem koncentratora:

■    inicjalizacja: a = (1 1 ... 1), h = (1 1 ... 1),

■    w pętli:

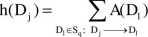
oraz

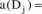
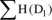
D|eS_q: D_:->Dj

■    znormalizuj h oraz a (będziemy stosować normalizację sumy składników do 1).

Ogólniej:

■    h = ALa = ApLL^Th,

■    a = pL^Th = ApL^TLa,

Sposoby rozwiązania:

■    Oblicz h oraz a iteracyjnie, zakładając dla każdej strony jednostkowe wartości początkowe dla roli koncentratora i autorytetu (w kolejnych krokach otrzymywane wektory h oraz a mnoży się przez odpowiednio LL^T lub L'L),

■    Rozwiąż układ równań, przyrównując wartości Ap lub oblicz wartości własne macierzy LL^T (L^TL) i przyjmij za rozwiązanie wektor własny odpowiadający największej wartości własnej (principle eigenvector).

Eksperymenty pokazują, że zbiór-korzeń powinien mieć ok. 200 stron, a żeby uzyskać dobre przybliżenie

wartości h oraz a wystarczy 5 iteracji.

-3-