365606334

Opracowanie konstrukcji osiowej pompy wspomagania serca

Zapisanie równania pędu dla prędkości uśrednionych, przez podstawienie do niego powyższych zależności skutkuje pojawieniem się w tym równaniu dodatkowego członu -tzw. tensora naprężeń turbulentnych, zwanego tensorem naprężeń Reynoldsa:

Opracowanie konstrukcji osiowej pompy wspomagania serca

T,

= ~P

u V vV

w'u'

u V

vV

wV

u'w' v'w' • w'w'

Do obliczeń zastosowano model k-epsilon, jeden ze standardowych modeli o dużej stabilności i dokładności wystarczającej dla większości inżynierskich obliczeń projektowych. Występuje on w wielu wariantach. Tu zastosowano model „Realizable k-epsilon". Model ten wykorzystuje koncepcję tzw. lepkości turbulentnej dla wyrażenia tensora naprężeń Reynoldsa w funkcji uśrednionych parametrów przepływu. Tensor naprężeń Reynoldsa wyrażony jest za pomocą aproksymacji Boussinesqa:

T, =    • v + pk)l

gdzie:

- współczynnik lepkości turbulentnej,

S - tensor prędkości deformacji, S = - (Vv + Vv^T ),

2^V ’

k - energia kinetyczna turbulencji, k = -(u'² +v'² +w'²)-

2^V ’

Dyskretyzacia równań ruchu cieczy

Równania algebraiczne rozwiązywane są numerycznie za pomocą metody objętości

skończonych. Metodę tę można w skrócie opisać następująco:

-    Obszar przepływu podzielony jest na niewielkie komórki zwane objętościami skończonymi.

-    Równania ruchu cieczy scałkowane są numerycznie dla każdej z objętości skończonych, przy czym wartość parametrów przepływu dla danej objętości przypisana jest do jej punktu środkowego.

-    Równania, scałkowane dla wszystkich objętości skończonych, tworzą układ równań algebraicznych, rozwiązywany w sposób iteracyjny.

Równania modelu "Rigid Body Motion"

Równanie ruchu środka masy ciała sformułowane w globalnym układzie

współrzędnych:

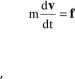
gdzie:

m oznacza masę ciała, f wynikową siłę działającą na ciało v jest prędkością środka masy.

402