3893820476
§§] Funkcja przynależności
=101x1
Nazwa zbioru rozmytego: [większość | Gęsta przestrzeń rozważań |
Funkcja trapezoidalna Funkcja Gaussowska j Funkcja użytkownika... ]
ia: [5J"
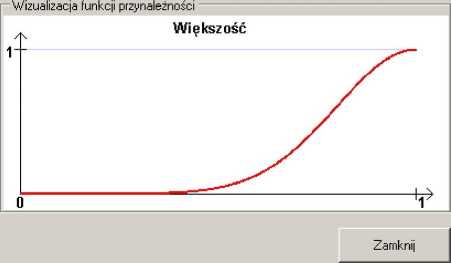
Rysunek 18: Funkcja przynależności kwantyfikatora „większość”
20
Wyszukiwarka
Podobne podstrony:
Sumą zbiorów rozmytych A,B Q X jest zbiór rozmyty A U B o funkcji przynależności: dla każdego x 6
Zbiór rozmyty (ang. fuzzy set) to obiekt matematyczny ze zdefiniowaną funkcją przynależności, która
img099 8.1. Postawienie zadania i podstawowe założenia 99 Q optymalna funkcja przynależności C Rys.
img039 39 3.4. Podział funkcji przynależności dach rozpoznawania przeznaczonych do konkretnych zasto
img041 41 3.4. Podział funkcji przynależności spotykanych w literaturze trzeba tu zachować umiar i w
img071 71 6.3. Wybór liniowej funkcji przynależności 3) prosty w realizacji algory
img073 73 6.3. Wybór liniowej funkcji przynależności procedurę linrec (obj, var rec); begin for i :=
img087 7.1. Podstawowe sformułowanie metody funkcji potencjalnych 87 Rys. 7.2. Funkcja przynależnośc
img099 8.1. Postawienie zadania i podstawowe założenia 99 Q optymalna funkcja przynależności C Rys.
7 Wizualizacja funkcji przynależności Poniżej przedstawione są wyglądy stworzonej kontrolki
Rysunek 15: Funkcja przynależności trapezoid * gauss Rysunek 16: Funkcja przynależności complement(g
8 Interfejs konfiguratora Parametry kwantyfikatora — Funkcja przynależności Kwantyfikator
Spis rysunków 1 Diagram klas funkcji przynależności (MembershipFunction)
więcej podobnych podstron