4831622755
314 Primoż Krivic
La methode de transformation de CARSON-LAPLACE a ćtó appliąuee par differents auteurs pour le calcul de diffusivitć, notamment en milieu poreux: M. Bonnet etJ. Schneider (1969), R. Degallier (1969), P. Peau-d e c e r f (1973), mais aussi en milieu fissure: J. C. G a r n i e r et C. L. Clarion (1967), M. Razack, C. Drogue, C. Romariz et C. Al-meida (1980).
2.2. Evolution de formę sinusoidale 2.2.1. Nappe captive
La propagation d'ondes pićzomćtriques dans l’aquif£re cótier peut <Rre representee par la rćsolution de l'equation differentielle de base de 1’hydro-dynamique souterraine, avec les conditions aux limites suivantes (J. B o u s -sinesą, 1877; J. Ferris, 1951):
h (x, t) = ho sin j Pour x = 0 et h (x, t) — 0 pour x = <x>
ho etant la demi amplitudę et to la periode de fluctuation du plan d’eau librę.
En faisant les memes hypotheses que dans le chapitre precedent, on obtient la solution suivante pour le mouvement de la surface pićzomśtrique dans une nappe captive (modele BOUSSINESQ):
h (x, t) = ho e~3ąxfl sin 2 n (t/to — x/l) avec 1 = |/4 n to T/Ś — longueur d'onde
d’ou la demi amplitudę h, des fluctuations de surface pićzometrique a la distance x du rivage:
hx - ho
et la vitesse V de transmission de 1’onde:
V - x/t =. L'to = 1;4 .t T/to S
la diffusivitó D = T S peut etre aisćment calculee, — soit a partir de 1'amortissement de 1'amplitude:
D
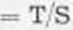
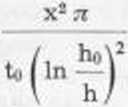
— soit k partir du dephasage:
D
T/S
tox8
4 TT t*
Cette demarche, tres classique, a partir de l equation de BOUSSINESQ, a ete reprise et developpśe par J. Ferris (1951), puis largement utilisće pour 1’interprćtation des fluctuations periodiques dans les nappes alluviales (G. Trupin -1969-, R. Degallier -1969-, E. De Cazenove -1971-,
Wyszukiwarka
Podobne podstrony:
3.3 Methode de collecte des donnees et d’analyse La methode de collecte des donnees dont nous ferons
314 CHOLŚRA comme le souligne Stewart, la vieille methode de preparation des vaccins choleriąues a p
RACTERIOLOGIE 151 borateurs out, dans une notę ulterieure, attribue une certaine valeur h la methode
page0349 WROŃSKIEGO ŻYCIE I PRACE. 839 87. Lagrange Cli. Exposition critique de la
— 341 — Les acides volatils, recherchćs par la methode de Du-claux, paraissaient etre faits d’un mel
44 3.3 La selection des participants Dans cette section seront expliqućs la methode de recrutement q
151 En outre, si on reporte la methodologie de cette methode de resolution mathematiąue dans notre e
5 • iborees dans la methodologie de recherche. Ces analyses gravitent autour des ćlements des strate
213 pendant une pleine insolation, un fragment de la plagę de la grandeur de 1 X ll 2 m environ, fut
guerir la volonte de Thomme, et qui lui tombe en partage pour le rendre fils de Dieu en Tincorporant
La coordination de chaque cours etait assuree par une equipe composee du directeur de 1’institution
318 Primoż Krivic la plus longue a dure du 25. 10. 1978 au 12. 12. 1978, soit 49 jours. Cctte period
Number of platform: Nous sommes a la gare de.............. Usual departure time: Le temps du depart
58 LA VOIX DE SAINT-CORENTIN Le 8 Septembre 1898, prenait place pour la premiere fois. au choeur, un
IZ METHODOLOGIE DE LA PREVISION DE L1ACCROISSEMENT ET DE LA PRODUCTION On peut y distinguer ąuatre ć
więcej podobnych podstron