5768158334

17

Materiały do kursu STATYSTYKA I ZASTOSOWANI A KOMPUTERÓW - semestr zimowy 2000/2001.

♦    Około 68% powierzchni pod krzywą mieści się w granicach jednego odchylenia standardowego na prawo i lewo od średniej

#    Pole obszaru w granicach od 1,96 odchylenia standardowego na lewo od średniej do 1,96 na prawo obejmuje 95% powierzchni pod krzy wą, a od 2,58 na lewo do 2,58 na prawo obejmuje 99% całkowitej powierzchni pod krzywą, przy czy m odpowiednio 5% i 1% mieści się poza tymi granicami.

Wszystkie rozkłady normalne mają taki sam podstawowy (dzwonowaty) kształt, różnić się mogą jedynie co do średnich i odchyleń standardowych. Średnią rozkładu może być dowolna wartość, podobnie jego odchylenie standardowe mierzyć może dowolna, nieujemna wartość.

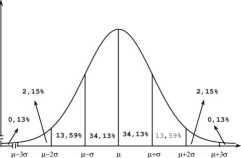
Rozkład IQ N (100,16)_|___

i    68    84    100    116    132    164

Jednostlii Z j    !    j    !    j    j

STANDARYZACJA WYNIKÓW

Aby dokonać standaryzacji wyników musimy dysponować pomiarem co najmniej na skali przedziałowej.

Dodanie/odjęcie stałej od zbioru wyników zmienia ich średnią, ale nie zmienia odchylenia standardowego. Mnożenie/dzielenie przez stalą k zmienia zarówno średnią jak i odchylenie standardowe wyjściowego zbioru wyników.

Używając powyższych transformacji dodawania/odejmowania oraz mnożenia/dzielenia danego zbioru wyników przez stalą k, można przekształcić każdy rozkład (pod warunkiem, że jego odchylenie standardowe nie wynosi zero) w rozkład o średniej równej zero i odchyleniu standardowym wynoszącym jeden. Takie przekształcenie rozkładu nazywa się standaryzacją.

Rozkłady nie posiadające średniej w punkcie zero i odchylenia standardowego równego jeden noszą nazwę niestandaryzowanych rozkładów normalnych. Aby taki rozkład przemienić w standaryzowany rozkład normalny konieczna jest transformacja surowych wyników na standaryzowane w yniki „Z”. Wykonuje się ją w oparciu o następujący wzór:

wynik - średnia odchylenie stand .

czyli Z =

X-M

s

Rozkład ten ma taki sam kształt jak rozkład niestandaryzowany. Własnością standary zowanego rozkładu normalnego jest to, że obszar pod krzywą równy jest jedności. Proporcja