5895613390

<>

Lotnik i Automobilista

Rozpatrzymy teraz kolejno wymienione trzy rodzaje lotu.

Zawieszenie. Zawieszenie jakiegokolwiek bądź przyrządu może w wypadku najprostszym nastąpić pod działaniem parcia wiatru na powierzchnię pochyłą, u ocowaną na linie, jednym swym końcem przywiązanej do punktu nieruchomego ¹).

Warunki równowagi przyrządu, w ten sposób zawieszonego, określają wzajemny stosunek sił pomiędzy sobą, które, jak wiadomo, powinny dawać w sumie geoi etrycznej wypadkową, równą zeru, oraz nie wytwarzać żadnego momentu.

Ponieważ na przyrząd działają trzy siły, a mianowicie ciężar przyrządu G_y parcie wiatru R (prncłopad* _c]₀ płaszczyzny) i siła napięcia liny F_y więc z warunków równowagi wynika, że

te p - -

t or a

cS

Oyf.Sl

O

I

Badając następnie to równanie, dochodzimy do kilku nader ciekawych wniosków, kt »rc przytaczam poniżej, opuszc 'ając całkowicie prowadzące do nich operacje matematyczne.

Znajdujemy przedeu , ;tkic ., że latawiec dla wniesienia się na największą wysokość (dla której kąt {3 jest również największym) powinien być pochylony do poziomu pod pewnym kątem a, ściśle określonym przez równanie:

/or 'i, \b 1

JO

G

SI

Kąt ten nie zależ)' od wymiarów latawca, lecz tylko od wielkości

w

o

którą nazywamy obciążeniem jednostkowem_} oraz od prędkości wiatru V.

Przypuść ny następnie, że chcemy znaleść kąt ₀ przy kt rym J3 = o (to znać \ linja jest poZi >nią); znajdziemy go łatwo z równania fj). Jeżeli zaś jednocześnie prędkość wiatru b Izie odpowiadała warunkowi (8) czyli

ws⁷’ stkie trzy siły muszą pr^cinać się w jednym punkcie O (n . 7), oraz rzuty ich na dwie osie pn itopadłr \ -winny równać się w sumie zeru, czyli:

R cos a — G F sin [3 o    (7)

R sin a —F cos _t3 = o    (/).

Kąt a nst w tym wypadku kątem pochylenia płaszcz; ny *Si> do poziomu, a kąt (3 odpowiada kątowi pochylenia liny do po''*p>mu w miej-( jej umocowania do płaszczv ny latawca C. ²)

Jeżeli do powyższych dwóch równań dodamy formułkę, określającą opór powietrza w zależności od kąta pochylenia płaszczyzny płaskiej

R = KSV² J (a)    (6),

więc dla danych warunków, to zn. dla danych G, S i V_y będziemy mogli znaleść zależność pomiędzy obydwoma kątami a i (3.

Dla znacznych kątów zderzenia (a) można w powyższej formułce przyjąć w przybliżeniu, ■godnie z propozycją Duchemin’a,

K = o, /

2 sin a

/ ' ~ ;/²"

Z równań (7),    (/) i (/>) znajdujemy tedy

z łatwością, :

¹) Nic r natrujemy tu t. zw. ni :\ idów Iż jjzy- * d powietrza, ’ tórc. p iwnic, wv ia • uf 'łr jj sp •-jU ntr r \ ' . c -c ^w awa_v za\vi< 'onemi nicrti-liomo, o v    ą ⁿi r'%

‘ » Kąt t * k" la się wi ile równania stycznei do linii łań< jc’ owej, < <    1 j( ’ ak w t miejscu mó..i<' nie

będzie >, ponic\. iż zaprov idziłoby to nas w zby. s >m-plikow. nc rozprav y matematyczne.

/(«)

\ / /o. G.

^v te *

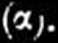
o

więc znaleziony kąt a₀ będzie odpowiadał na* większemu kątowi, przy którym lata w ‘ r j< v *^1 jest w stanie unieś< się z zit ii.

Kąt ten, jak łatwo jest się przekonać, okr^ a się z równania

*g *0 = V i = °>7°7    !

i znajdujemy

JS° *5 i?”

Inaczej mówiąc, dowolny latawiec, niezależnie od jego wagi i wielkości powierzchni, pochylony do poziomu pod kątem większym, niż a (/) }( , nie będzie w stanie unii : ;ię z ziemi. Odwrotnie możemy znal ai najmniejszą prędko? wiatru, potrzebną do wzniesienia si latawca.

Określamy ją z warunku, że V powinno być większe od

V > V m in    5

Najmniej :a szybk< • zależną więc jest od obciążenia jednostkow ro.

Poprzestając na rozpatrzeniu tych kilku najf *''wni# js'• ch wniosków, które w^j ływają zc st « *ci lośc ‘ weg • r "»i iv< ’ c nnikc w, warun-

kuj ic ;*t 11 ^1 iv\	a\ ■	nia	latawca, d« r’ r
te k ’.^a uwag	co do s	' F}	budowv t( 0 ro-•
• ‘ * p^r ) M 1« V Łat w ni w	id*/i *ć,	VI	zadc ■•*»''/) ni^<*'*ic
warunko 1 rc \> a* .	^fi» 7.go/	nic	z p id m n i p
wy j r *wnaniair^:,	samo pr	— -	. nie j^ >t j~

^A w ^farozają< Prędki wiatru nie i* * wic ” .ą stałą, lecz, jak wskazują badania, zn.’