606616409

176

PRZEMYSŁ CHEMICZNY

23 (1939_;

przy porównaniu z równaniem Staudingera^ł,l:

wynika, że V_Q jest prop>rcjonalne do K_mM.

Pytanie czy V,, w konkretnym przypadku jest uwarunkowane solwatacją (Fikentscher i Mark) czy kształtem cząstki (Staudinger) zostaje narazie otwarta. Jednak szereg badaczy¹⁰) stara się ująć V₀ jako funkcję kształtu cząstki.

Należy zaznaczyć, że także S a k u r a d a¹⁷) wprowadził pojęcie, odpowiadające V₀ Bredćego i Booysa/, nazwane objętością właściwą cząstki koloidowej.

Przekształceniu przez Bredćego i Booysa uległy jeszcze następujące równania:

2 5

Fikentscher (9): 75 h* + k = — V₀.

Bungenberg de Jong, K r u y t, Lens (10): k_x = 2,5 V_c] a = log k_t.

Baker (11): a k = 2,5 V₀.

Najdogodniej jest posługiwać się jako znormalizowaną stałą objętościowością V₀, będącą wyobrażeniem fizycznym (objętość właściwa cząstki koloidowej).

Wszystkie powyższe równania za wyjątkiem równania (1) P a p k o v a przechodzą w równanie Einsteina.

Równanie Einsteina w drugim przybliżeniu, sformułowane przez niego samego, dla cząstek kulistych brzmi:

A r r h e n i u s a¹⁸): log Tj_wzg| = k c_v .... (6) Fikentschera i Marka¹*):

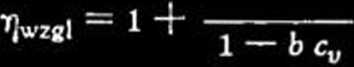
S a k u r a d a¹⁷):

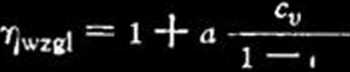
(7)

(8)

Fikentscher a¹⁹): l^v2 7]wzgl

75 fc*

___+ k

1 + 1.5 kc_v I

• (9)

TJwzgl = 1 + 2.5 <p + 4,4 tp²

jednak co do teoretycznej wielkości spółczynnika przy drugiej potędze są zdania podzielone ^f» *), możliwość stosowania tego wzoru do bardziej stężonych roztworów jest ograniczona, dlatego starano się wyprowadzić empirycznie, a potem uzasadnić teoretycznie nowe równania, o większej ilości stałych.

I tak Bredće i de Booys¹⁰) podają wzory:

l + 2,5 V'

7jwzgl    —    (12a)

Bungenberg de Jong, H. Kruyt i J Len s**):

log

^: a

+ bc_v

(10)

Bakę r*¹):

TJwzgl = (1 + ac_v ) k

(U)

C_V = V’ c_v (1 4-V' c_v) «-    (12b)

a = nowa stała:

Bredće i de Booys¹⁰):

l°g Y]_W7g| — k‘ c_v

łtc_v = k’c_v ( 1 + c_v + 0,1 U c_v )    ¹    (13)

Otrzymano następujące wartości stałych: P a p k o v (1):

K. H. Klaassens, R. H. Houwink i C. F. Yeeneman s^,ł):

²A

2,3

1 —a

^K = -^V.‘c-*,

7j_w2g|

_ K,+K₂p«

1 + p

6

(14)

Phi lipo ff i Hess (3): [Y]] = 2,5 V₀. O. Kratky i G. Saito (2):

= V 75 V₀

Arrhenius (6):

Fikentscher i Mark (7): kb =* 2,5 V₀. Sakurada (8): a'f =* 2,5 V₀.

^1S) H. Staudinger, Die hochmolekularen organi-schen Verbindungen, Berlin, Julius Springer 1932.

^If) R. E i s e n s c h i t z, Z. physik. Chem. A. 158, 78 (1931); 163, 133 (1933); W. K u h n, tamże 161, 1 (1932); Kolloid-Z. 62. 269‘(1933); E. Guth .Kolloid-Z. 74. 147 (1936).

¹⁷)    I. Sakurada, Kolłoid Z. 63, 311; 64, 195 (1933).

¹⁸)    S v. A r r h e n i u s, Z. physik. Chem. 1, 285 (1887).

¹⁹)    H. F i k e n t s c h e r, Cellulosechem. 13, 58 (1932). *•) H. G. B u n g e n b e r g de J o n g, H. R. K r u y t

i J. Lens, Kolloidchem. Beih. 36, 429 (1932).

•■) F. Baker, J. Chem. Soc. 103, 1653 (1913).

gdzie K_x, K_t, aa₂, i p są nowe stałe. Stałe te w określonych zakresach lepkości częściowo odpowiadają i stają się identyczne ze stałymi równania Papkova.

Bredće i de Booys²³) sprawdzali równania: Arr heniusa (6), Finkentschcra (9), Bu ngen-berg de Jonga (10), Philipoffa i Hessa (3), B r e d ć e, van B e r g e n a i de Booysa (12), Bredće i de Booysa (4) Papkova(l) Houwink a, Klaassens a, Veenemansa(14)na roztworach nitrocelulozy, acetylocelulozy, żelatyny, gumy arabskiej i kauczuku (ciała wysokocząsteczkowe naturalne).

Stwierdzono najlepszą stałość dla danego szeregu pomiarów dla k =* lepkość własna Fikentschera (9), także dość dobrą stałość dla V_c wg równania (4).

Inne równania spełniają warunek stałości tyłko dla ograniczonego zakresu stężeń.

Przeprowadzono porównawcze badanią dla szeregu ciał

**) R. Houwink i K. H. Klaassens, Kolloid-Z. 79, 138 (1937); R. Houwink, Ocstcrr. Chem. Zgt. 40, 472 (1937).

**) H. L. Bredće i J. dc Booys, Kolloid-Z. 79, 43 (1937).