6295505278

WYDZIAŁ TRANSPORTU I ELEKTROTECHNIKI

UNIWERSYTETU TECHNOLOGICZNO - HUMANISTYCZNEGO

przy wyznaczaniu półpłaszczyzn opisanych warunkami (b) i (c). Z warunków dodatkowych (d) i (e) wynika, że zbiór rozwiązań dopuszczalnych dla modelu znajduje się w pierwszej ćwiartce układu współrzędnych. Znajdujemy obszar w którym spełnione są warunki ograniczające modelu, będzie to część wspólna wszystkich półpłaszczyzn. Dla rozpatrywanego przykładu warunki ograniczające zasadnicze i dodatkowe spełnione są w trójkącie ABC i jest to zbiór rozwiązań dopuszczalnych (ZRD) modelu. Został on zaznaczony na rys. 10.1.

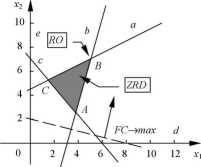
Rys. 10.1. Zbiór rozwiązań dopuszczalnych i rozwiązanie optymalne

Następnie wykreślamy funkcję celu (FC). Aby narysować prostą wyznaczającą (FC) można przyjąć dla niej dowolną wartość (wartość tę przyjmuje się tak aby była ona dogodna do jej narysowania). Załóżmy, że wartość jej wynosi 2. Rysujemy prostą o równaniu (na rys. zaznaczona linią przerywaną):

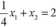
Wyznaczając rozwiązanie maksymalizujące funkcję celu będziemy przesuwać równolegle daną prostą. Można zauważyć, że wartość FC rośnie gdy rośnie X\ i x₂. Kierunek wzrostu FC zaznaczono strzałką. Prostą należy przesuwać równolegle w górę układu współrzędnych. Największą wartość w zbiorze rozwiązań dopuszczalnych funkcja celu osiągnie w punkcie B. Współrzędne tego punktu można wyznaczyć rozwiązując układ równań.

J-x,+2x₂ =9 [7x, - 2x₂ =21

Rozwiązaniem układu jest punkt o współrzędnych *i=5, x₂=7 a więc współrzędne punktu są rozwiązaniem optymalnym (RO) dla podanego modelu. Dla punktu B o podanych współrzędnych spełniony jest układ warunków ograniczających i funkcja celu przyjmuje wartość największą równą 22