6815960224
Ze wzorów tych wynika, iż przy Tr >0 obserwuje się pochylenie linii komutacji w lewo, zaś przy Tr < 0 w prawo - w stosunku do odpowiednich linii komutacji dla Tr = 0 (por. wzory (5.8) i (5.9)). Stosowny podział płaszczyzny fazowej pokazano na rys. 5.11. Rysunek ten dotyczy praktyczne ważniejszego przypadku Tr>0.
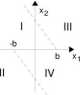
Rys. 5.11 Płaszczyzna fazowa i linie komutacji
W obszarach I i II obowiązują równania (5.10)-(5.12), zaś w obszarach III i IV - równania (5.13)-(5.15), wyprowadzone w punkcie 5.2.1. W tym miejscu można skorzystać z odpowiednich rozwiązań owych równań, także podanych w punkcie 5.2.1. Tak postępując, sformułowano następujący warunek na parametr cyklu granicznego, występującego w rozważanym układzie sterowania (zob. rys. 5.12)
BkpTp\n\(Bkp+x$)/(Bkp-xZ)\-2(Tp-Tr)x;=2b. (5.62)
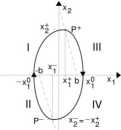
Rys. 5.12. Reprezentacja cyklu granicznego na płaszczyźnie fazowej
Podobnie jak w punkcie 5.2.1, opis cyklu granicznego uzyskuje się, łącząc odpowiednie fragmenty trajektorii fazowych. Rozwiązanie równania (5.62) pozyskuje się na drodze numerycznej, przy czym z dwóch możliwych rozwiązań należy wybrać to, które spełnia nierówność <Bkp. Analiza wzoru (5.62) prowadzi do następujących wniosków:
• Funkcja (lr) jest funkcją monotonicznie malejącą.
• Funkcja Xy(Tr) = b-TrX2(Tr) jest funkcją monotonicznie malejącą (por. rys. 5.12).
• Amplituda cyklu granicznego (7A, opisana wzorem
Wyszukiwarka
Podobne podstrony:
404 [1024x768] 413 NIEKTÓRE RÓWNOWAGI W ROZTWORACH ELEKTROLITÓW Z równań tych wynika, ic przy długoś
W wyniku reakcji tłuszczu ze stęż. NaOH w obecności etanolu i w podwyższonej temperaturze obserwuje
Kolendowicz23 ■ Funkcje c (n) przedstawiono w postaci wykresów na rys. 15-18. Z wykresów tych wynika
skrypt134 137 Przy zmianie stanu skupienia ze stałego w ciekły, obserwuje się dla wszystkich elali s
Skrypt PKM 1 00151 302 Przy obrotach dowolnie zmiennych w okresie T o gdzie T L0 = J n(t)cf». o Prz
S6300979 99 Przykłady Z równości tych wynika, że funkcja g ma w punkcie *o * 2 nieciągłość pierwszeg
Przy sporządzaniu wykresów funkcji trygonometrycznych korzystaliśmy ze wzorów sin (90 s+cc) = cos oc
Twierdzenia wynikające ze wzorów na środki ciężkości: 1 Środek ciężkości bryły, figury płaskiej lub
Z badań przeprowadzonych w latach 80-tych przez M Portera wynika, iż istnieją potencjalnie 3 skutecz
0000094 2 Jednakże okazało się, że kondensacja tych składników następuje nie przy udziale CoA-SH, a
28 (266) Ze wzorów (3.35) oraz (3.40) wynika, że przedziały ufności i predykcji mają większą rozpięt
jak i szczawianie amonu. Z oznaczeń tych wynika, że użyty kwas szczawiowy jest dokładnie 2-wodny, a
118 B. Baronf Z. Garczarczyk 4. Schemat blokowy identyfikacji Ze wzorów (20) i (21) wynika, że Jeżel
więcej podobnych podstron