8482348971

-    H - wysoki, L - niski i przypiszemy im stany logiczne w następujący sposob H=1 i L=0, to otrzymamy logikę dodatnią.

Przy przyporządkowaniu odwrotnym tzn.:

-    H - wysoki, L - niski, ale wartość stanów H=0 i L=l, otrzymamy logikę ujemną.

Przy takiej reprezentacji podstawowe funkcje logiczne można realizować za pomocą odpowiednich układów elektronicznych posiadających jedno lub wiele wejść oraz jedno wyjście (rysunek 1.4).

Rysunek 1.4. Układ elektryczny realizujący funkcję logiczną

Ponieważ istnieje wiele rozwiązań układowych wspomnianego układu, dla uproszczenia wprowadzono symbole oznaczające funkcję logiczną realizowana przez układ, a nie mówiące nic o jego budowie wewnętrznej.

0-^-1 I y=x1+x

oĄyJ—*

oĄ \    y=x1+x:

—*

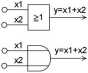
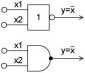
Rysunek 1.5. Symbole podstawowych funkcji logicznych

Zauważmy, że pomimo pewnej realizacji układowej opis wejść i wyjść układu pozostał zgodny z opisem logicznym i nie odzwierciedla poziomów napięć występujących w układach.

1.2. Inne funkcje logiczne

Poprzednio pokazano, że dowolną funkcję logiczna można przedstawić za pomocą odpowiedniej kombinacji funkcji OR, AND i NOT. Istnieją jednak funkcje złożone, które w technice występują na tyle często, że nadano im własne nazwy. Funkcjami tymi są:

funkcja równoważności, przyjmuje wartość y = 1 wówczas, gdy obie zmienne wejściowe są sobie równe:

y = EQUIV(x_l ,x₂) = x^c~₂ + x,x₂

- funkcja nierównoważności, jest negacją równoważności; y -1 gdy zmienne wejściowe są różne.

y - ANTIV(x,,x₂) = x,x₂ + x, x₂

Z tablicy prawdy wynika jeszcze inna interpretacja funkcji nierównoważności; funkcja ta jest zgodna z funkcja OR dla wszystkich wartości z wyjątkiem przypadku, gdy wszystkie zmienne wejściowe są równe jeden. Dlatego nosi ona nazwę EXCLUSIVE OR (EXOR) lub sumy modulo 2 (MOD 2)

y = EXOR(x_], x₂) = x,x₂ + x, x₂

Zgodnie z tym funkcję równoważności można nazwać funkcją EXCLUSIVE NOR (EXNOR) y = EXNOR(x_x, x₂) = x, x₂ + x,x₂