8857686412
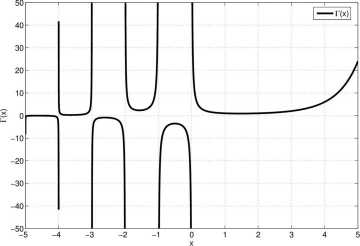
Rysunek 2.1: Przebieg wartości funkcji T(x)
Definicja 2 [162] Jednoparametrową Funkcją Mittaga-Lefflera nazywamy funkcją zmiennej zespolonej zdefiniowaną w następujący sposób:
T(ak + 1)
E°(z) = Y
k=0
Dla a = 1 otrzymujemy
*M-Ei
czyli tradycyjną funkcję eksponencjalną.
Na rysunkach 2.2 i 2.3 przedstawione są przykładowe przebiegi funkcji Mittaga-Lefflera. Na rysunku 2.2 jest to przebieg jednoparametrowej funkcji Ea(x) dla a = 1,1.2,1.5, na rysunku 2.3 natomiast przedstawiony jest przebieg dla a = 1,0.7,0.5.
Rozszerzeniem definicji jednoparametrowej funkcji Mittaga-Lefflera jest dwuparametrowa funkcja Mittaga-Lefflera. Jest ona zdefiniowana następująco:
Definicja 3 Dwuparametrową funkcją Mittaga-Lefflera nazywamy funkcję zmiennej zespolonej określoną w następujący sposób:
16
Wyszukiwarka
Podobne podstrony:
Rysunek 2.2: Przebieg wartości funkcji Ea(x) dla a = 1,1.2,1.5 Rysunek 2.3: Przebieg wartości funkcj
Rysunek 1.2: Wykres wartości zamknięć indeksów z 60-ciu tygodni.1.2 Funkcja straty Do obliczeń w kol
6.2. Definicja gry Algorytm MINIMAX Zasada algorytmu minimax dla dwóch graczy MAX i MIN Wartości fun
Definicja 0.5.5 Dla zmiennej X o wartościach {0,1,2,...} funkcję 1x(z) = E{zx) = J2 zlp(i) i=0 dla z
POCHODNE FUNKCJI Narzędzie służące do badania przebiegu zmienności wartości funkcji, określonej na
Scan0050 62 Funkcje jako relacje Definicja 6.3 PrzeciwdziedzinąWf funkcji nazywamy zbiór wartości fu
skanuj0029 (15) • Niektóre wartości funkcji trygonometrycznych ar o(o°) f(*) §m f(9T) sin
Image055 zerojedynkowe zmiennych niezależnych. Ostatnia kolumna jest przeznaczona do zapisania warto
Image156 Tablica wartości funkcji F(x) dla określonego współczynnika podziału N Tablica
Image178 wejścia przetwornika C/A. Zapisując w pamięci 256 słów, odpowiadających kolejnym wartościom
Image301 Wartość funkcji dla sumy i przeniesienia bez korekcji i z korekcją wyniku dodawania w zapis
img298 Obecnie wszystkie zmienne niebazowe mają dodatnie kryterium simpleks, a więc wartości funkcji
skanuj0066 (45) Rozdział 6. ❖ Równania i układy równań algebraicznych 81 3. Sprawdź, czy wartości fu
img082 82 6. Metody aproksymacyjne Rys. 6.8. Dychotomie liniowe dla m = 2 oraz N = 4 Tabela 6.1. War
img130 130 Wszystkie te punkty leżę wewnątrz koła K i dlatogo obliczamy wartości funkcji g w tych pu
więcej podobnych podstron