• Współczynnik alfa Cronbacha

(Cronbach alpha)

Szacowanie rzetelności testu w oparciu o wariancję jego części składowych (pozycji, podtestów, części testu itp.).
alfa Cronbacha, przedstawia się następująco:

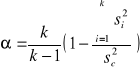
k = liczba pozycji testowych

s_c² = wariancja wyników ogólnych testu

= suma wariancji pozycji testowych.

Rozważmy przykład zastosowania wzoru alfa Cronbacha. W tabeli zamieszczono wyniki pięciu osób z pewnego testu, w którym zakres dostępnych odpowiedzi wyrażony był na skali Likerta (od 1 do 5). W kolejnych kolumnach przedstawiono odpowiedzi każdej osoby, obliczenia wariancji dla całego testu oraz wariancji poszczególnych pozycji testowych.

W celu obliczenia wariancji należy odjąć każdy wynik od średniej, a następnie uzyskaną wartość podnieść do kwadratu. Wariancję stanowi stosunek sumy odchyleń wyników od średniej podniesionych do kwadratu do liczby osób badanych minus jeden. W tabeli 5.2 przedstawiono kolejne kroki obliczania wyników wariancji całego testu i poszczególnych pozycji testowych.

Kolejne kroki obliczeń, oznaczono jako A, B, C, D w dolnym wierszu tabeli 5.2. Wszystkie obliczenia przebiegają w ten sam sposób, zarówno jeżeli chodzi o wariancję całego testu, jak i poszczególnych pozycji. W kroku A należy zsumować wszystkie wyniki otrzymane (całego testu i kolejnych pozycji), a następnie (krok B) policzyć średnią tychże. Znając średnią wartość możemy odjąć od niej każdy poszczególny wynik otrzymany, jak też zostało to uczynione w kolumnie oznaczonej (X-
). Otrzymane w ten sposób wartości należy podnieść do kwadratu (wynik tego działania przedstawia w tabeli 5.2. kolumna (X-
)²). W kroku C należy zsumować wszystkie wartości podniesione do kwadratu, a następnie podzielić je przez liczbę osób badanych minus jeden (krok D). W ten sposób uzyskano wariancje odpowiednio dla całego testu oraz każdej kolejnej pozycji.

Tabela 5.2. Wyniki poszczególnych pozycji testowych oraz wyniki ogólne dla 5 osób badanych w teście składającym się z 4 pozycji.

Osoby	Pozycje testowe	Cały test	Pozycja 1	Pozycja 2	Pozycja 3	Pozycja 4
	1 2 3 4	Xc (Xc- c)(Xc- c)^2	X1 (X1 - 1) (X1- 1)^2	X2 (X2- 2)(X2- 2)^2	X3 (X3- 3) (X3- 3)^2	X4 (X4- 4) (X4- 4)^2
1 2 3 4 5	3 1 1 2 2 4 5 4 5 5 4 5 4 2 2 3 1 3 3 1	7 -5 25 15 3 9 19 -7 49 11 -1 1 8 -4 16	3 0 0 2 -1 1 5 2 4 4 1 1 1 -2 4	1 -2 4 4 1 1 5 2 4 2 -1 1 3 0 0	1 -2 4 5 2 4 4 1 1 2 -1 1 3 0 0	2 -1 1 4 1 1 5 2 4 3 0 0 1 -2 4
Kolejne kroki A. obliczeń: B. C. D.		 Xc = 60 c = 12 (Xc - c)^2= 100 sc^2= 25	 X1 = 15 1 = 3 (X1- 1)^2= 10 s1^2= 10/4	 X2 = 15 2 = 3 ( X2 - 2)^2= 10 s2^2= 10/4	 X3 = 15 3 = 3 ( X3- 3)^2= 10 s3^2= 10/4	 X4 = 15 4 = 3 ( X4 - 4)^2= 10 s4^2= 10/4

X = wynik otrzymany przez daną osobę

= średnia wyników otrzymanych

X = suma wyników otrzymanych

(X-
) = odchylenie wyniku otrzymanego przez daną osobę od średniej

(X-
)² = kwadrat odchylenia wyniku otrzymanego przez daną osobę od średniej

(X-
)² = suma kwadratów odchyleń wyników otrzymanych od średniej

s² = wariancja wyników

W powyższym przykładzie wariancja każdej pozycji wynosi 2,5, zatem suma wariancji wszystkich pozycji równa się 10. Wariancja całego testu wynosi 25. Podstawiając uzyskane dane do wzoru 5.5 otrzymujemy:

=0,8

---