Instytut Automatyzacji procesów Technologicznych

i Zintegrowanych Systemów Wytwarzania

Wydział Mechaniczny Technologiczny

Politechnika Śląska w Gliwicach

• PODSTAWY STEROWANIA ROBOTÓW I MASZYN

Projekt

• PROSTE ZADANIE KINEMATYKI

Grzegorz Ozimek, grupa 3, semestr 1

Kierunek: Automatyka i robotyka

• I

• Wstęp teoretyczny

Kinematyka manipulatora.

Proste zadanie kinematyki jest to zadanie statyczno-geometryczne polegające na obliczeniu pozycji i orientacji członu roboczego manipulatora. Mając dane wszystkie współrzędne konfiguracyjne należy obliczyć pozycję danego punktu związanego z robotem (przede wszystkim chwytaka) względem globalnego układu współrzędnych. Zadanie to traktowane jest jako zadanie odwzorowania opisu położenia manipulatora w przestrzeni współrzędnych konfiguracyjnych na opis w przestrzeni współrzędnych kartezjańskiej.

 

Wyprowadzenie przekształceń dla poszczególnych członów.

Zadaniem jest znalezienie przekształcenia, określającego układ {i} względem układu {i-1}. Na ogół przekształcenie to będzie funkcją czterech parametrów członu. Dla każdego danego robota przekształcenie to będzie funkcją tylko jednej zmiennej, pozostałe trzy parametry są ustalone i wynikają z konstrukcji mechanicznej. Określając układ odniesienia dla każdego członu dokonano podziału zadania kinematyki na n podzadań. W celu rozwiązania każdego z tych podzadań, przykładowo ^i-1T_i , podzielono każde z nich na cztery pod-zadania. Każde z tych czterech przekształceń będzie funkcją tylko jednego parametru członu i będzie na tyle proste, że będzie można napisać jego postać przez sprawdzenie.

Zastosujemy cztery, kolejne przekształcenia, mianowicie:

1. Obrót wokół osi Z_i-1 o kąt θ_i,

2. Przesunięcie wzdłuż osi Z_i-1 o wielkość λ_i,

3. Przesunięcie wzdłuż osi Z_i o wielkość l_i,

4. Obrót wokół osi X_i o kąt α_i.

• Macierz przekształcenia A_i:

Macierz A_i opisuje przejście z układu {i-1} do kolejnego układu { i }, a więc:

• A_i = ^i-1T_i

zgodnie z notacją Hartenberga-Denavita, kolejnymi przekształceniami jakie wykonuje się przy przejściu z układu {i-1} do { i } są:

• obrót wokół osi zi-1 o kąt θi zatem:
• przesunięcie wzdłuż osi zi-1 o λi (identyczne przekształcenie jest dla przesunięcia wzdłuż osi zi-1 o li):
• obrót wokół osi xi o kąt αi:

Przekształcenie A_i będzie wyglądało, więc tak:

A_i = Rot(z_i-1, θ_i)Trans(0,0,λ_i)Trans(l_i,0,0)Rot(x_i,α_i),

 

a macierz A_i będzie miała taką postać ogólną :

 

Parametrami Hartenberga-Denavita są zatem:

• θ_i, λ_i, l_i, α_i

przy czym:

θ_i = zmienna konfiguracyjna dla pary obrotowej,

λ_i = zmienna konfiguracyjna dla pary przesuwnej,

l_i = const; α_i = const.

θ_i dla pary przesuwnej przyjmuje wartości stałe, a dla pary obrotowej λ_i = const.

• II

• Dane do zadania

θ₁ = -60 [*]

θ₂ = 30 [*]

θ₃ = 60 [*]

d₁ = λ₁ = 2.5 [m]

d₂ = λ₂ = 1 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

Schemat manipulatora wraz z globalnym, oraz lokalnymi układami współrzędnych:

• III

• Wyznaczanie macierzy translacji oraz obliczenia

Obliczenia główne:

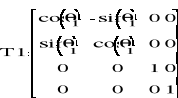
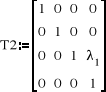
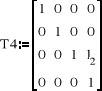
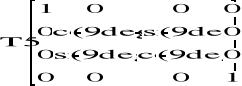
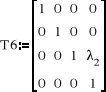
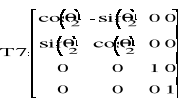
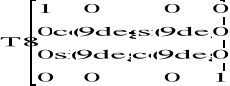
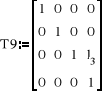
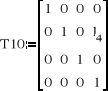
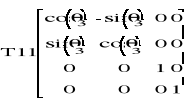
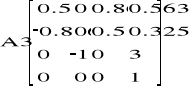
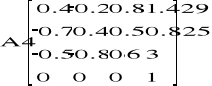
Zatem punkt kiści: A5(2.153 ; 1.07 ; 3.26).

Obliczenia dodatkowe dla 5 różnych zestawów wartości:

1)

θ₁ = 0 [*]

θ₂ = 30 [*]

θ₃ = 60 [*]

d₁ = λ₁ = 2.5 [m]

d₂ = λ₂ = 1 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

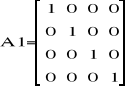
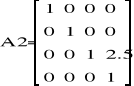
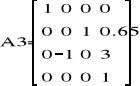
Zatem punkt kiści: A5(0.15 ; 2.4 ; 3.26).

2)

θ₁ = -20 [*]

θ₂ = 10 [*]

θ₃ = 20 [*]

λ₁ = 0.82 [m]

λ₂ = 0.32 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

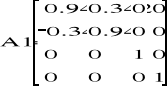
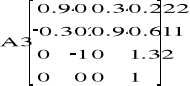
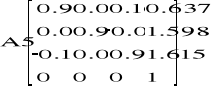
Zatem punkt kiści: A5(0.637 ; 1.598 ; 1.615).

3)

θ₁ = -30 [*]

θ₂ = 15 [*]

θ₃ = 30 [*]

λ₁ = 1.23 [m]

λ₂ = 0.48 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

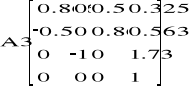
Zatem punkt kiści: A5(1.007 ; 1.589 ; 2.02).

4)

θ₁ = -40 [*]

θ₂ = 20 [*]

θ₃ = 40 [*]

λ₁ = 2.05 [m]

λ₂ = 0.8 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

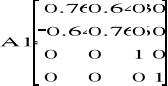
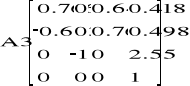
Zatem punkt kiści: A5(1.493 ; 1.619 ; 2.832).

5)

θ₁ = -50 [*]

θ₂ = 25 [*]

θ₃ = 50 [*]

λ₁ = 2.5 [m]

λ₂ = 1 [m]

l₁ = 0.65 [m]

l₂ = 0.5 [m]

l₃ = 0.3 [m]

l₄ = 0.75 [m]

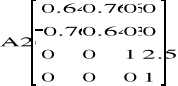
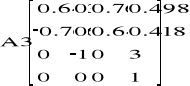
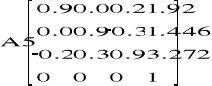
Zatem punkt kiści: A5(1.92 ; 1.446 ; 3.272).

• IV

• Wnioski

Sensem zadania prostego kinematyki manipulatora jest znalezienie macierzy X, która odpowiada za przekształcenie układu {0} - związanego z nieruchomą podstawą manipulatora, w układ {n+1} - związanego z chwytakiem (narzędziem, kiścią) ostatniego ramienia w łańcuchu.

Zatem dzięki prostemu zadaniu kinematyki można w miarę prosty sposób wyznaczyć położenie ostatniego członu manipulatora robota (kiść - oprzyrządowanie technologiczne robota), a także wszystkich pośrednich par kinematycznych. Metoda ta jest bardzo prosta, a zarazem efektywna.

---