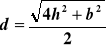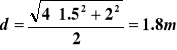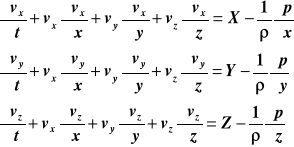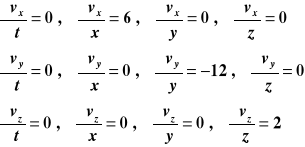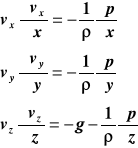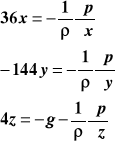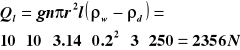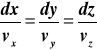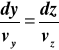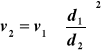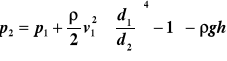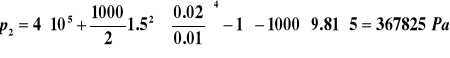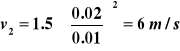26.11.2009
Kolokwium z MP - nr 1, zestaw 2 - IŚ WBiA ZUT, s.3, r. 2009/2010
Wiedząc, że gęstość wody morskiej ρw≅1030 kg/m3, a gęstość lodu ρL≅900 kg/m3, obliczyć jaka część góry lodowej znajduje się nad powierzchnią wody.
Dane jest naczynie prostopadłościenne o wymiarach b=2m (długość) i c=1m (szerokość), wypełnione wodą o objętości V=3m3 i masie m=3600 kg, które zjeżdża bez tarcia ruchem jednostajnie przyspieszonym z przyspieszeniem a=3 m/s2 po równi pochyłej o kącie nachylenia α=0.5 rad. Obliczyć maks. ciśnienie wywierane przez ciecz na tylną ścianę naczynia.
Ruch cieczy w potencjalnym polu sił ciężkości określony jest składowymi prędkości: vx=6x, vy=-12y, vz=2z. Wyprowadzić równanie rozkładu ciśnienia przy założeniu, że początek układu OXYZ leży na powierzchni swobodnej cieczy (Oś Z skierowana do góry), a ciśnienie barometryczne wynosi pb
Korzystając z prawa Archimedesa obliczyć, jak duży ciężar można przeprawić przez rzekę za pomocą tratwy zbudowanej z 10 okrągłych kłód drewnianych o średnicy 20 cm i długości 3 m każda. Gęstość drewna przyjąć równą 750 kg/m3 a gęstość wody 1000 kg/m3
Określić równanie linii prądu dla przepływu o następującym ustalonym polu prędkości :
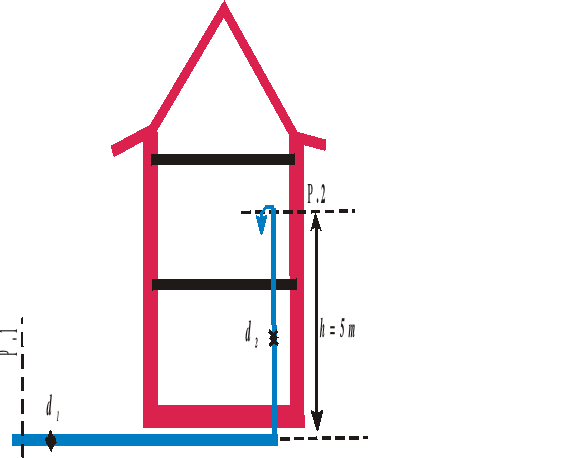
Woda jest dostarczana do domu rurą o średnicy d1=2 cm, pod ciśnieniem p1 = 4·105 Pa. Rura prowadząca na piętro na wysokości 5 m ma średnicę d2 = 1 cm. Po odkręceniu kranu na piętrze prędkość wody w rurze zewnętrznej wynosi v1 = 1.5 m/s. Obliczyć ciśnienie i prędkość wody w kranie. (12p)
Rozwiązanie :
|
Z rys. objętość góry lodowej V=V1+V2 Ciężar góry jest równy ciężarowi wypartej wody: V·ρL=V2·ρw Dalej już tylko przekształcenia w kierunku uzyskania V1/V:
V·ρL=(V-V1)·ρw V1·ρw=V(ρw- ρL) |
Szukane: pmax = ? [N/m2] |
Dane: b=2 m, c=1 m, V=3 m3, a=3 m/s2, α=0.5 rad, g=9.81 m/s2, ρ=1000 kg/m3, pa=1013 hPa =1.013105 Pa Układ współrzędnych: punkt OXYZ leży na pow. swobodnej cieczy w połowie szerokości naczynia - niezależnie od zmiany kata nachylenia pow. swobodnej, punkt ten podczas ruchu leży zawsze na powierzchni swobodnej cieczy. Podpowiedź: skorzystać z podstawowego równania hydrostatyki. Pole jednostkowych sił masowych: X=-a·cos α, Y=0, Z=g-a·sin α. Współrzędne p-ktu A: xA=-d•cos α, yA=y, zA=d•sin α, d - odl. A od OXYZ, wyzn. z tw. Pitagorasa dla trójkąta o bokach przyprostokątnych b/2 i h, gdzie h=V/(bc) |
Rozwiązanie:
Podstawowe równanie hydrostatyki: |
Wstawiając do niego występujące w zadaniu pole sił masowych mamy: |
Z lokalizacji początku układu OXYZ wynika, że p(0,0,0)=pa czyli C=pa |
Ogólna postać równania ciśnienia jest zatem równa: |
Średnia głębokość wody w naczyniu: h=V/(bc) czyli h=3/(2·1)=1.5m |
Odległość d p-ktu A od OXYZ jest przeciwprostokątną trójkąta o wierzchołkach A, b/2 i OXYZ, czyli |
Współrzędne p-ktu A są zatem: xA=-d·cos α, yA=y, zA=d·sin α |
Wstawiając te współrzędne do równania ciśnienia, otrzymujemy:
|
Liczbowo: =0.5 rad =(0.5/Pi)180≈28.65º |
sin ≈, cos2 ≈0.77
|
Wskazówki: Wektor siły masowej jest równy:
Podpowiedź: Wyznaczyć pochodne składowych pola prędkości, wstawić je i wektor siły do równań Eulera. |
Następnie wymnożyć odpowiednie równania przez dx, dy i dz i dodać je stronami. Otrzymane równanie będzie obustronnie różniczką zupełną, którą trzeba scałkować a stałą wyznaczyć z podanego warunku . |
||
Rozwiązanie: równania Eulera mają postać:
|
Zadane pole prędkości skutkuje tym, że:
|
||
i dostajemy uproszczony układ:
Przemnożymy te równania |
przez przyrosty dx. dy i dz:
|
dodajemy obustronnie, dostając różniczki zupełne:
To można już scałkować, otrzymując:
|
|
Stała C wynika z warunku: dla (0,0,0) p=pb, |
i ostatecznie szukane równanie ciśnienia ma postać:
|
||
|
Podpowiedź: Nośność = Siła Wyporu (przy zadanym zanurzeniu) - Ciężar Własny. |
Rozwiązanie: Dane: n =10 kłód drewnianych o średnicy d = 20 cm i długości l = 3 m każda. Gęstość drewna ρd = 750 kg/m3, gęstość wody ρw = 1000 kg/m3, przyspieszenie grawitacyjne g = 10 m/s2. |
Siła wyporu działająca na tratwę ma zrównoważyć ciężar tratwy z ładunkiem: Fwyporu=Qtratwy+Qladunku czyli Qladunku =Fwyporu-Qtratwy Maksymalna siła wyporu jest wtedy, gdy tratwa jest cała zanurzona w wodzie - objętość wypartej wody jest wtedy równa objętości tratwy i wynosi V=n·π·r2·l. |
Ostatecznie: |
Wykorzystując powyższą zależność, otrzymujemy, że nośność:
|
vx = 0, vy = -4z, vz =2y
dla elementu płynu, który w pewnej chwili przechodzi przez punkt (0,16,4).
Wykorzystać równanie różniczkowe linii prądu (będą tylko dwie składowe), następnie scałkować (będą to różniczki o zmiennych rozdzielonych). Stałą C wyznaczać z podanego warunku.
Rozwiązanie: równanie różniczkowe linii prądu:
Wstawiając podane prędkości dostajemy: |
Po scałkowaniu otrzymujemy szukane linie prądu:
|
Z warunku przechodzenia przez punkt C=288 |
czyli równ. linii prądu w płaszczyźnie y-z ma postać: |
|
Podpowiedź: Piszemy równanie Bernoulliego dla przekroju 1 na rurze prowadzącej do domu i przekroju 2 na rurze w mieszkaniu na wysokości kranu. Skorzystać także z równania ciągłości.
|
Rozwiązanie:
czyli
|
Aby wyrazić niewiadomą v2 przez v1, trzeba skorzystać z równania ciągłości: Daje to po podstawieniu do r. Bernoulliego:
|
Wyszukiwarka
Podobne podstrony:
MP kol 2 z2 z rozw
MP kol 2 z1 z rozw
kolokwium2, grupa 2 kol 2
kolokwium2, grupa 2 kol 2
Tematyka kolokwium z MP - materiał wykładów, simr, mechanika płynów, mechanika płynów
Kolokwium mp opracowane pytania(1)
MP 7 modele wielorównaniowe. rozw, metody prognozowania
kolokwium poprawa, kol i egz przyklady
kolokwium 2010 01 07 rozw
06 04 05 kol 5 kwiet rozw ch
kolokwium nr 1 2011 2012 rozw
071NI-Kol-04032009-2005, astronawigacja, astro, Przykładowe kolokwia z astronawigacji, Kolokwium nr
legalne wzory kolokwium 5 id 26 Nieznany
kol 1 rozw
Wyniki kolokwium zaliczeniowego z kompleksowej ochrony lasu dla studentów III roku OZL, Dokumenty se
2006 arytmetyka kolokwium 2 rozw errata
więcej podobnych podstron