RACHUNEK PRAWDOPOBOBIEŃSTWA I STATYSTYKA MATEMATYCZNA

Laboratorium 1 i 2

rok akademicki 2011/12

Obliczanie prawdopodobieństwa i statystyk z rozkładów zmiennych losowych

skokowych (dyskretnych) - LABORATORIUM 1 i zmiennych losowych ciągłych - LABORATORIUM 2

Celem ćwiczenia jest zapoznanie:

• z zastosowaniem arkusza kalkulacyjnego Excel do obliczania prawdopodobieństwa i statystyk z rozkładów dla zmiennych losowych dyskretnych (skokowych) i zmiennych losowych ciągłych,

• z wybranymi rozkładami prawdopodobieństwa (kształt, właściwości, zastosowanie) dla zmiennych losowych dyskretnych i ciągłych,

• interpretacji wyników.

Materiały opracowane z wykorzystaniem między innymi następujących źródeł:

[1] Ostasiewicz S., Rusnak Z., Siedlecka U.: Statystyka. Elementy teorii
i zadania. Wydawn. Akademii Ekonomicznej we Wrocławiu, Wrocław 2006.

[2] M. Sobczyk, Statystyka, PWN, Warszawa, 2007.

[3] W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski, Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, cz. I, Rachunek prawdopodobieństwa, PWN, Warszawa 2002.

[4] W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski, Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, cz. II, Statystyka matematyczna, PWN, Warszawa 2002.

Pojęcia podstawowe

Przez zmienna losową można rozumieć zmienną, która w wyniku doświadczenia przyjąć może jedną z wartości zbioru liczb rzeczywistych i to z określonym prawdopodobieństwem.

Przykłady: ilość energii elektrycznej zużywanej dziennie przez wydział produkcyjny; rzeczywista rezystancja wybranego losowo rezystora spośród produkowanych seryjnie rezystorów; liczba uszkodzonych podzespołów w wyniku awarii.

Zmienna losowa skokowa (dyskretna) - jest to zmienna, która posiada skończony lub policzalny zbiór wartości, najczęściej są to liczby naturalne (np. liczba oczek wyrzucona za pomocą kostki do gry). Każda zmienna losowa dyskretna jest jednoznacznie charakteryzowana za pomocą dystrybuanty i funkcji rozkładu prawdopodobieństwa zmiennej losowej dyskretnej.

Zmienna losowa ciągła - jest to zmienna, która może przybierać dowolne wartości liczbowe (rzeczywiste) z pewnego przedziału, nieskończonego i niepoliczalnego (np. mierzone natężenie prądu). Każda zmienna losowa ciągła jest jednoznacznie charakteryzowana za pomocą dystrybuanty i funkcji rozkładu gęstości zmiennej losowej ciągłej.

Dystrybuanta zmiennej losowej X to funkcja F(x) zmiennej rzeczywistej x, która wyznacza prawdopodobieństwo tego, że zmienna losowa X przyjmie w uporządkowanym zbiorze:

x₁ ≤ x₂ ... ≤ x_i ≤ ...x_n-1 ≤ x_n wartość mniejszą od x:

F(x) = P(X < x)    dla każdego

Własności dystrybuanty:

• przyjmuje wartości z przedziału 0 ≤ F(x) ≤ 1 dla
  ;

• jest funkcją niemalejącą, tzn. dla x₁ < x₂ zawsze F(x₁) ≤ F(x₂);

• jest funkcją lewostronnie ciągłą;

•  
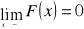
  oraz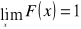
  

Parametry zmiennej losowej są to liczby charakteryzujące wartości, jakie może przybierać zmienna losowa. Najważniejszymi parametrami zmiennej losowej są wartość oczekiwana i wariancja.

Wartość oczekiwana (przeciętna) E(x) - jest to wartość, wokół której skupiają się realizacje zmiennej losowej uzyskiwane w wyniku wielokrotnego powtarzania eksperymentu.

Właściwości wartości oczekiwanej:

• wartość oczekiwana stałej równa się tej stałej:

E(C) = C;

• wartość oczekiwana sumy dwóch zmiennych losowych X i Y równa się sumie wartości oczekiwanych tych zmiennych:

E(X + Y) = E(X) + E(Y);

• jeżeli dwie zmienne X i Y są niezależne, to wartość oczekiwana iloczynu zmiennych jest równa iloczynowi wartości oczekiwanych tych zmiennych:
  E(X·Y) = E(X) · E(Y);

• wynika stąd również zależność:
  E(C·X) = E(C) · E(X) = C·E(X)

Wariancja zmienne losowej V(X) - miara rozproszenia wartości zmiennej losowej wokół wartości średniej, jest określona wzorem:

V(X) = [X - E(X)]²

V(X) = E(X ²) - E(X)²

Własności wariancji:

• wariancja stałej równa się zeru:
  V(C) = 0;

• wariancja iloczynu stałej i zmiennej losowej:
  V(CX) = C ²V(X);

• jeżeli dwie zmienne X i Y są niezależne, to wariancja sumy (różnicy) tych zmiennych jest równa:
  
  .

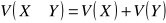
Odchylenie standardowe σ zmiennej losowej X jest to pierwiastek z jej wariancji:

Charakterystyka zmiennej losowej dyskretnej

Dla zmiennej losowej skokowej dystrybuanta jest równa:

Funkcją rozkładu prawdopodobieństwa dla zmiennej losowej skokowej (dyskretnej) X, która przybiera wartości: x₁, x₂, ..., x_n i odpowiadające im prawdopodobieństwa p₁, p₂, ..., p_n, definiuje się jako:

P(X = x_i) = p_i i = 1, ..., n

Parametry rozkładu zmiennej losowej dyskretnej:

Wartość oczekiwana zmiennej losowej skokowej:

- gdy zmienna X przyjmuje n wartości,

- gdy zmienna X przyjmuje przeliczalnie wiele wartości.

Wariancja zmiennej losowej skokowej:

lub

Odchylenie standardowe σ zmiennej losowej:

Współczynnik zmienności
:

Współczynnik skośności A_σ:

Medianą Me zmiennej losowej X - nazywamy wartość x, która spełnia układ równań:

i

Modalną Mo zmiennej losowej X - nazywamy wartość x, której odpowiada największe prawdopodobieństwo realizacji.

Wybrane rozkłady zmiennej losowej dyskretnej - laboratorium 1

1.Rozkład dwumianowy

Rozkład dwumianowy (Bernoulliego, binominalny) służy do wyznaczenia prawdopodobieństwa, tego, że podczas realizacji n doświadczeń osiągniemy k sukcesów (k ≤ n):

gdzie
jest kombinacją:
.

Dystrybuanta:

Wartość oczekiwana: E(X) = np

Wariancja: V(X) = npq

Zmienna losowa o rozkładzie dwumianowym opisuje eksperyment noszący nazwę prób Bernoulliego - dlatego rozkład ten nazywany jest także rozkładem Bernoulliego.

Eksperyment polega na przeprowadzeniu n (n ≥ 2) niezależnych doświadczeń, wynikiem może być tylko jedno z dwóch możliwych stanów: sukces lub porażka:

• prawdopodobieństwo stanu, który został uznany za sukces jest takie samo w kolejnych doświadczeniach (p), prawdopodobieństwo niepowodzenia q łączy się z p zależnością: p + q = 1;

• doświadczenia są niezależne, tzn. wynik poprzedniego nie wpływa na wynik następnego;

Funkcja rozkładu dwumianowego zależy od dwóch parametrów: liczby doświadczeń n i prawdopodobieństwa sukcesu p;

• dla p = q = 1/2 rozkład dwumianowy jest symetryczny, dla p ≠ q rozkład jest asymetryczny, jeżeli p < 1/2 - prawostronnie asymetryczny, dla p > 1/2 - lewostronnie asymetryczny.

2. Rozkład Poissona

Rozkład ten został zaproponowany przez S. D. Poissona (1781-1840) w pierwszej połowie XIX wieku.

Rozkład Poissona jest szczególnym przypadkiem rozkładu dwumianowego, zachodzącym wtedy, gdy prawdopodobieństwo p sukcesu jest małe, a liczba realizacji n na tyle duża, że np = λ. Rozkład Poissona stosuje się jako przybliżenie rozkładu dwumianowego, gdy prawdopodobieństwo sukcesu jest mniejsze niż 0,2, a liczba doświadczeń jest równa co najmniej 20 ( W niektórych pozycjach literaturowych 30 lub nawet 50. Stawia się też niekiedy warunek na np =  λ, postulując by ten iloczyn nie przekraczał 5).

Rozkład prawdopodobieństwa:

Dystrybuanta:

Wartość oczekiwana:

E(X) = λ

Wariancja:

σ² = V(X) = λ

3. Rozkład hipergeometryczny

Z rozkładem hipergeometrycznym mamy do czynienia przy losowaniu bez zwracania z populacji skończonej.

Jeżeli prawdopodobieństwo sukcesu w kolejnych doświadczeniach się zmienia (np. losowanie bez zwracania) oraz z populacji liczącej N elementów pobieramy n-elementową próbę (n ≤ N), oraz że dokładnie R elementów ma wyróżnioną cechę (wylosowanie takiego elementu uważamy za sukces), to zmienną losową, która oznacza liczbę sukcesów, opisuje rozkład hipergeometryczny:

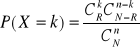
k = 0, 1, ..., min(R, n)

gdzie:

N - liczba elementów populacji;

R - liczba elementów w populacji mających interesującą nas cechę (liczba sukcesów w N elementowej populacji);

n - liczebność próby;

k - liczba sukcesów.

Wartość oczekiwana:

Wariancja:

gdzie:
i

Rozkład hipergeometryczny H(N, R, n) jest zbieżny do rozkładu dwumianowego B(n,p) - dla dużej populacji nie ma znaczenia, czy losowanie odbywa się bez zwracania, czy ze zwracaniem. Rozkład hipergeometryczny jest często wykorzystywany w statystycznej kontroli jakości.

Wybrane rozkłady zmiennej losowej ciągłej - laboratorium 2

Charakterystyka zmiennej losowej ciągłej

Dla zmiennej losowej ciągłej nie jest możliwe przypisanie wszystkim jej wartościom dodatnich prawdopodobieństw sumujących się do jedności. Możliwe jest jednak przyporządkowanie takich prawdopodobieństw przedziałom liczbowym, na przykład przedziałowi P(x < X < x + x), gdzie x jest długością pewnego krótkiego przedziału o początku w punkcie x.

Jeżeli Δx → 0 oraz istnieje granica funkcji f(x) w postaci:

to granicę tę nazywamy funkcją gęstości prawdopodobieństwa zmiennej losowej X lub krótko gęstością prawdopodobieństwa.

Prawdopodobieństwo tego, że zmienna losowa przyjmuje wartość z przedziału (a, b) - skończonego lub nieskończonego - jest całką funkcji gęstości prawdopodobieństwa w tym przedziale:

Jeżeli zmienna losowa X przybiera wartości z przedziału skończonego (a, b) lub nieskończonego (-∞,+∞) to funkcja gęstości f(x) musi spełniać warunki:

• f(x) ≥ 0 - funkcja musi być nieujemna

• 
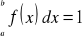
  oraz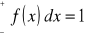
  

Prawdopodobieństwo tego, że zmienna losowa ciągła X przyjmie dokładnie wartość a (gdzie a jest dowolną stałą) jest równe zeru:

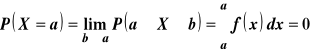
Nie oznacza to, że zdarzenie x = a jest niemożliwe, jest ono bardzo mało prawdopodobne, ponadto, prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość inną niż x = a jest równe jedności, co nie świadczy o tym, że jest ono pewne.

Należy je uważać za wysoce prawdopodobne.

Dystrybuanta zmiennej losowej ciągłej F(x) = P(X < x) - jest definiowana podobnie jak dla zmiennej losowej skokowej, z tym, że suma jest zastąpiona całką:

stąd

f(x) = F'(x)

przy warunku, że F(x) jest funkcją różniczkowalną.

Dla zmiennej losowej X przyjmującej wartości z przedziału (a,b):

Ponadto: 

Parametry zmiennej losowej ciągłej

Wartość oczekiwana:

Wariancja :
lub

Medianą Me zmiennej losowej ciągłej: - jest wartość, dla której spełniona jest równość:

F(x) = 1/2

Modalną Mo zmiennej losowej ciągłej - jest wartość, dla której funkcja gęstości f(x) osiąga maksimum.

Rozkłady ciągłe

1. Rozkład jednostajny

Zmienna losowa X ma rozkład jednostajny (prostokątny) w przedziale [a,b], jeśli jej funkcja gęstości jest określona wzorem:

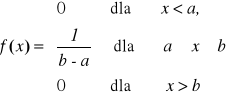
Dystrybuanta zmiennej losowej ciągłej o rozkładzie jednostajnym ma postać:

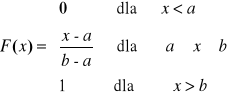
Wartość oczekiwana:

Wariancja:

Mediana

Brak modalnej, ponieważ funkcja gęstości nie ma maksimum.

2. Rozkład wykładniczy

Zmienna losowa X ma rozkład wykładniczy z parametrem λ, jeśli jej funkcja gęstości jest określona wzorem:

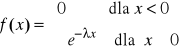
Dystrybuanta tej zmiennej jest:

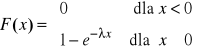
Wartość oczekiwana E(X)=1/λ ;

Wariancja V(X)=1/λ²;

Mediana Me=(-ln0,5)/ λ

Dominanta zmiennej losowej dla rozkładu wykładniczego nie istnieje, ponieważ funkcja gęstości nie ma maksimum.

3. Rozkład normalny

Zmienna losowa X ma rozkład normalny z parametrami μ i σ, jeśli jej funkcja gęstości jest określona wzorem:

Dystrybuanta:

Kształt funkcji zależy od wartości parametrów: μ i σ. Parametr μ przesuwa krzywą wzdłuż osi odciętych, natomiast parametr σ powoduje, że krzywa jest bardziej spłaszczona lub wysmukła.

Funkcja f(x) ma własności:

• jest symetryczna względem prostej x = μ, co oznacza, że spełniona jest zależność: P(X > μ) = P(X < μ) = 0,5

• w punkcie x = μ osiąga wartość maksymalną, która wynosi

;

• prawdopodobieństwo, że zmienna losowa X przyjmuje wartości z przedziału:

[μ - 3σ; μ + 3σ], jest w przybliżeniu równe jedności (reguła trzech sigm).

Reguła ta mówi, że praktycznie wszystkie wartości zmiennej losowej mieszczą się w przedziale [μ - 3σ; μ + 3σ]).

Wartość oczekiwana

Wariancja

Mediana i modalna

---