Prędkość kątowa i przyspieszenie kątowe
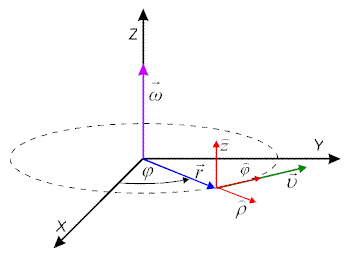
Ruch obrotowy wygodnie jest rozpatrywać w układzie cylindrycznym przyjmując, że oś
jest osią obrotu a ruch odbywa się w płaszczyźnie
. Ruch płaski rozpatrywaliśmy już w lekcji drugiej stosując biegunowy układ współrzędnych i rozkładając wektor prędkości na składowe: radialną i transwersalną, wzór (2.22). Kiedy mamy do czynienia wyłącznie z ruchem obrotowym, to prędkość radialna równa jest zeru i wektor prędkości punktu materialnego może być zapisany w postaci
|
(5.1) |
Skorzystaliśmy tu z relacji pomiędzy wersorami w układzie współrzędnych cylindrycznych (Rys.2.3.) i przemienności mnożenia wektora przez wielkości skalarne. W prawej części wzoru wprowadziliśmy wielkości
|
(5.2) |
Pierwsza z nich, to wektor prędkości kątowej skierowany wzdłuż osi obrotu, druga jest wektorem promienia wodzącego skierowanym od osi obrotu do poruszającego się punktu. Tak zdefiniowany wektor wodzący jest prostopadły do osi obrotu.
|
Zwróćmy uwagę, że wartość wektora prędkości kątowej równa jest pochodnej przemieszczenia kątowego względem czasu, zaś jego kierunek pokrywa się z osią obrotu. Zwrot wektora zgodny jest z regułą śruby prawoskrętnej. Przy zmianie kierunku ruchu obrotowego zwrot tego wektora zmieni się na przeciwny. Jeżeli prędkość kątowa zachowuje stałą wartość, to w ruchu tym możemy wyrazić moduł prędkości kątowej jako Jednostką prędkości kątowej jest radian na sekundę. |
Rys. 5.2. Określenie wektora prędkości kątowej |
|
Ruch obrotowy ze stałą prędkością kątową opisuje się także podając czas, w którym poruszające się ciało wykonuje jeden pełny obrót, czyli kiedy kąt obrotu wynosi
. Czas ten, oznaczany zwykle jako
, nosi nazwę okresu w ruchu obrotowym. Liczbę obrotów wykonanych przez ciało w czasie jednej sekundy, czyli odwrotność okresu, nazywa się częstotliwością i oznacza zwykle jako
lub
. Zapiszmy relacje pomiędzy tymi wielkościami.
|
(5.3) |
Jednostką okresu jest sekunda, jednostką częstotliwości jest jeden herc (Hz); jego wymiarem jest odwrotność sekundy.
Kiedy prędkość kątowa zmienia się w czasie mówimy o ruchu obrotowym przyspieszonym. Przyspieszenie kątowe,
, które charakteryzuje zmianę prędkości kątowej w czasie, określamy jako pochodną prędkości kątowej względem czasu, czyli drugą pochodną przemieszczenia kątowego względem czasu
|
(5.4) |
gdzie
. Kierunek wektora przyspieszenia kątowego określony jest więc przez kierunek zmiany prędkości kątowej.
Wartości prędkości i przyspieszenia kątowego wiążą się z wartościami składowych prędkości i przyspieszenia, które określiliśmy w lekcji drugiej. Wykorzystując wzór (2.22) i przyjmując, że prędkość radialna równa jest zeru mamy
|
(5.5) |
Prędkość kątowa wiąże się ze składową normalną wektora przyspieszenia. Wykorzystując wzory (2.36) oraz (5.5) otrzymujemy
|
(5.6a) |
gdzie promień krzywizny toru
we wzorze (2.36) odpowiada wartości bezwzględnej określonego wzorem (5.2) wektora
.
Wartość przyspieszenia kątowego wiąże się ze składową styczną wektora przyspieszenia, wzór (2.36), zależnością
|
(5.6b) |
przyjmujemy bowiem, że wartość
nie zmienia się w czasie.
Wyszukiwarka
Podobne podstrony:
7 Dynamika ruchu obrotowego bry Nieznany
dynamika ruchu obrotowego
Dynamika ruchu obrotowego, 6
Dynamika ruchu obrotowego, 5
Dynamika ruchu obrotowego, 5
Dynamika ruchu obrotowego bryly
Dynamika ruchu obrotowego, 4
III01 Dynamika ruchu obrotowego bryly sztywnej
2?DANIE DYNAMIKI RUCHU OBROTOWEGO BRYŁY SZTYWNEJ
7 Dynamika ruchu obrotowego właściwe
1 Badanie dynamiki ruchu obrotowego 12
07 Dynamika ruchu obrotowego bryly sztywnej, Domumenty
pawlikowski, fizyka, dynamika ruchu obrotowego i drgającego
Dynamika ruchu obrotowego, 1
Dynamika ruchu obrotowego
6 Dynamika ruchu obrotowego ciala sztywnego, Politechnika Wrocławska Energetyka, I semestr, Fizyka 1
14 DYNAMIKA RUCHU OBROTOWEGO
7 Dynamika ruchu obrotowego bry Nieznany
Dynamika ruchu obrotowego bryły sztywnej (2)
więcej podobnych podstron