Rok akademicki 1996/97	Laboratorium z fizyki
Nr ćwiczenia: 55	Temat: Identyfikacja pierwiastka promieniotwórczego przez wyznaczenie górnej granicy widma Beta
Wydział: Elektronika Kierunek: E-nika i Telekom. Grupa: E03	Imię i nazwisko: Tomasz Zalewski
Data wykonania	Ocena		Data zaliczenia	Podpis
	T
	S

1. Zasada pomiaru.

Podczas przemiany następuje jądrze przemiana neutronu w proton i elektron, który wylatuje z jądra (cząsteczka β). Ponadto w czasie tej przemiany powstaje jeszcze jedna cząstka o masie spoczynkowej i ładunku równym zeru oraz spinie równym: .

Jest to cząsteczka zwana neutrinem (albo antyneutrinem).

Energia rozpadu jest dzielona między te dwie cząstki. Zatem na energię pojedynczego rozpadu promieniotwórczego składać się będzie energia cząstki β oraz energia odpowied-niego neutrina (lub antyneutrina).

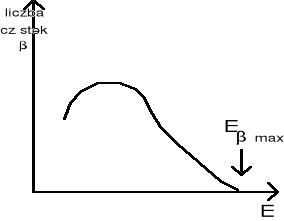
Widmo energetyczne cząstek β emitowanych podczas rozpadu jest widmem ciągłym, o ściśle określonej energii maksymalnej E_{β max} , charakterystycznej dla danego pierwiastka promieniotwórczego.

Podstawą identyfikacji pierwiastka promieniotwórczego jest poznanie zależności między strumieniem cząstek, które przeszły określoną warstwę absorbenta i grubością absorbenta, na podstawie której wyznaczamy maksymalną energię cząstki β. Maksymalny zasięg będą miały cząstki o takiej energii.

Maksymalny zasięg wyznacza się z prawa absorbcji cząstek :

gdzie:

             
- współczynnik masowy pochłaniania w cm 2/g

             R - grubość warstwy absorbenta w g/cm 2

      N0 , N - strumień cząstek b w nieobecności i po przejściu absorbenta

Po wyznaczeniu ilości cząstek zarejestrowanych dla różnych grubości absorbenta, można wykreślić krzywą ln N = f(R)

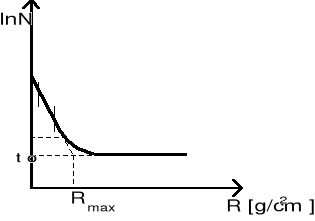
     przy pomocy której, przez ekstrapolację do wartości tła, otrzymujemy maksymalny zasięg      cząstek . Teraz pozostaje tylko na jego podstawie ustalić rodzaj pierwiastka.

2. Schemat układu pomiarowego.

3. Ocena dokładności pojedynczych pomiarów.

Za błąd pomiaru impulsów n_i została przyjęta ±1 cyfra wyświetlana licznika z odczytem cyfrowym. Oznacza to, że poszczególny pomiar obarczony jest błędem ±1 impuls.

Wartość R_i podana jako stała traktowana była jako wartość dokładna.

4. Tabele pomiarowe.

Lp.
	229
1	216	221	133	0	11,53	4,89	0,09
	218
	149
2	142	152	91	20,25	9,54	4,51	0,10
	166
	122
3	95	113	68	40,50	8,25	4,22	0,12
	121
	72
4	76	75	45	60,75	6,71	3,81	0,15
	77
	56
5	57	57	34	81,00	5,83	3,53	0,17
	58
	43
6	46	45	27	101,25	5,20	3,30	0,19
	47
	35
7	32	34	20	121,50	4,47	3,00	0,22
	34
	39	39	24	-	4,90	3,18	0,20

5. Przykładowe obliczenia wyników pomiarów wielkości złożonej.

6. Rachunek błędów.

7. Zestawienie wyników pomiarów.

     Wyniki pomiarów wraz z błędami pomiarowymi znajdują się w punkcie 4.

Odczytana z wykresu wartość maksymalnego zasięgu cząstek wyniosła około 96 [mg/cm²]. Wartość ta wyznaczona została na podstawie dwóch prostych pomocniczych nakreślonych pod największym i najmniejszym możliwym kątem (wynikającym z błędu
), a następnie poprzez wykreślenie trzeciej prostej będącej uśrednieniem prostych wyjściowych. Jak widać na wykresie maksymalny zasięg cząstek może wahać się w granicach: od 88 do 120 [mg/cm²]. Maksymalna energia cząstek odczytana z wykresu zależności
od
wynosi ok. 0,4 MeV.

A podstawie tabeli dołączonej do opracowania ćwiczenia możliwa jest identyfikacja pierwiastka. Pierwiastkiem o najbardziej zbliżonej wartości okazał się wolfram ¹⁸⁵W. Jego energia maksymalna wynosi 0,430 MeV.

Maksymalny zasięg cząstek	88÷120 [mg/cm^2]
Średni maks. zasięg cząstek	96 [mg/cm^2]
Maksymalna energia cząstek	0,4    [MeV]

     

8. Uwagi i wnioski.

Stosunkowo prosta metoda wyznaczania wartości z wykresów nie jest zbyt dokładną metodą. Przykładowo narysowanie w trochę niedokładny sposób linii pomocniczych wprowadza dużą niedokładność i w konsekwencji źle odczytaną wartość żądaną.

W ten sposób należało wyznaczyć wartość w ćwiczeniu poprzez ekstrapolację wykresu do wartości tła poprzez wyznaczenie dwóch skrajnie możliwych do poprowadzenia prostych. Przy nieznacznych przesunięciach prostych wkradała się niedokładność, a w związku z tym uśredniona prosta obu poprzednich również mogła nie być dokładna. Wykres został sporządzony wraz z błędami, które dotyczyły jedynie wartości lnN_iśr ponieważ R_i przyjęte było jako wartość dokładna i zależna tylko od ilości folii.

Niedokładność pomiaru mogła również wynikać z tego, że w trakcie pomiarów folie oddzielało powietrze, tak więc nie można powiedzieć że absorbent był jednorodny.

---