Rok akademicki: 19997/1998
|
Laboratorium z fizyki |
|||
Numer ćwiczenia: 63 |
Temat ćwiczenia: Procesy fizyczne w lampach elektronowych. |
|||
Wydział: elektronika Kierunek: elektr. i telekom. Grupa: 1.3 |
Imię i Nazwisko Jacek Rachwalski |
|||
Data wykonania: |
Ocena |
Data zaliczenia |
Podpis |
|
10. 03.1998 r. |
teoria |
|
|
|
|
sprawozdanie |
|
|
|
1. Wprowadzenie.
Prąd elektryczny może płynąć także bez udziału przewodzącego materiału np. w lampach elektronowych. W częściach metalowych obwodu z lampą elektronową prąd polega na ruchu swobodnych elektronów w kierunku przeciwnym do umownego kierunku prądu. By obwód był zamknięty, w przerwie między anodą i katodą muszą też płynąć elektrony w kierunku od katody do anody. Rozgrzana katoda wysyła więc swobodne elektrony tworzące prąd anodowy. Zjawisko to nosi nazwę termoemisji. Ponieważ elektrony mogą się swobodnie poruszać tylko wewnątrz metalu od wyjścia na zewnątrz są powstrzymywane siłami przyciągania jonów dodatnich metalu. Na granicy metal-powietrze istnieje więc nagła zmiana potencjału zwana barierą potencjału. By elektron mógł się z metalu wydostać, musi pokonać tę barierę, tzn. musimy mu dostarczyć pracy równej przyrostowi energii potencjalnej przy przejściu z metalu do próżni. Jeśli skok potencjału na granicy zetknięcia przewodnika z powietrzem wynosi U , praca będzie równa eU. Nazywamy ją pracą wyjścia elektronu z metalu. Jeśli wszystkie elektrony tworzące prąd w lampie elektronowej docierają do anody to mamy do czynienia z prądem nasycenia.
Doświadczenia wykazują iż gęstość prądu nasycenia jn wzrasta bardzo szybko wraz ze zwiększeniem temperatury katody. Na podstawie teorii kwantowej opisującej zjawisko termoemisji można obliczyć wartość gęstości prądu nasycenia. Wyraża ją wzór Richardsona - Dushmana :
gdzie:
T - temperatura bezwzględna w K
W - praca wyjścia
k - stała Boltzmanna
B - stała emisyjna zależna od stanu powierzchni metalu i stopnia jego
czystości
jn - gęstość prądu nasycenia
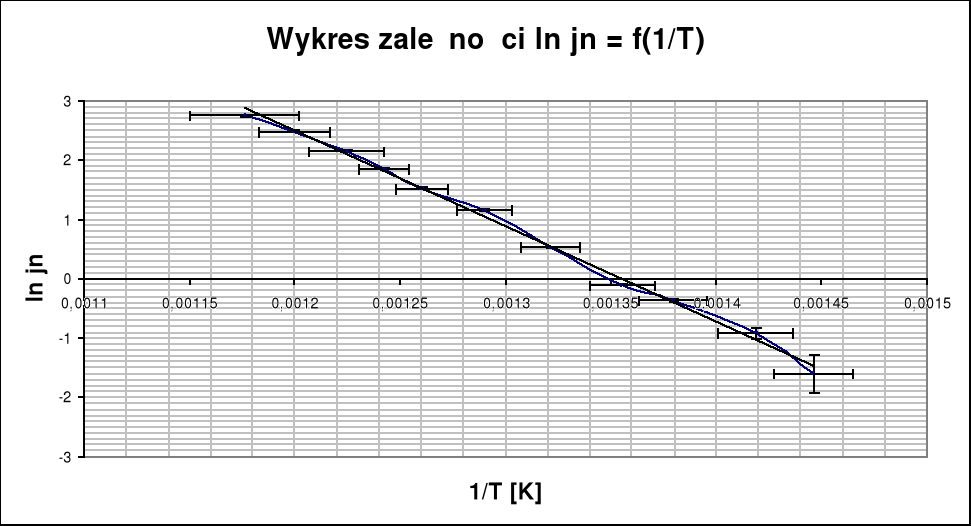
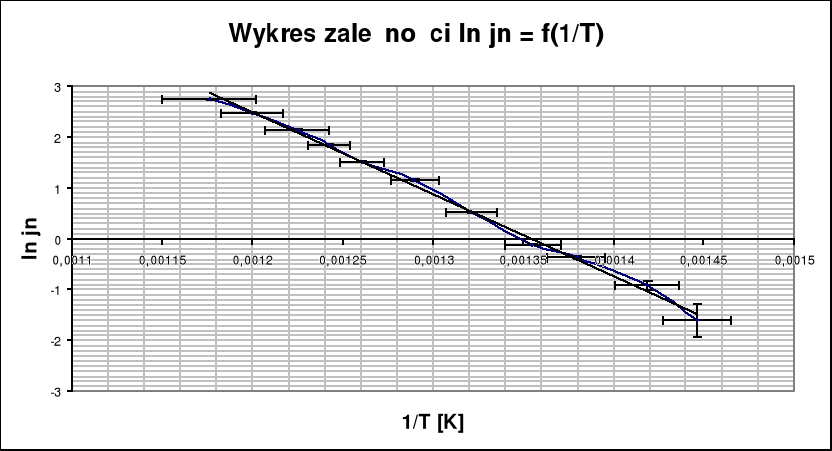
Pomiar prądu nasycenia In (jego gęstości jn) oraz znajomość temperatury katody pozwala znaleźć pracę wyjścia W [eV]. Można ją wyznaczyć na podstawie wykresu zależności:
![]()
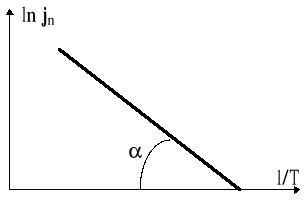
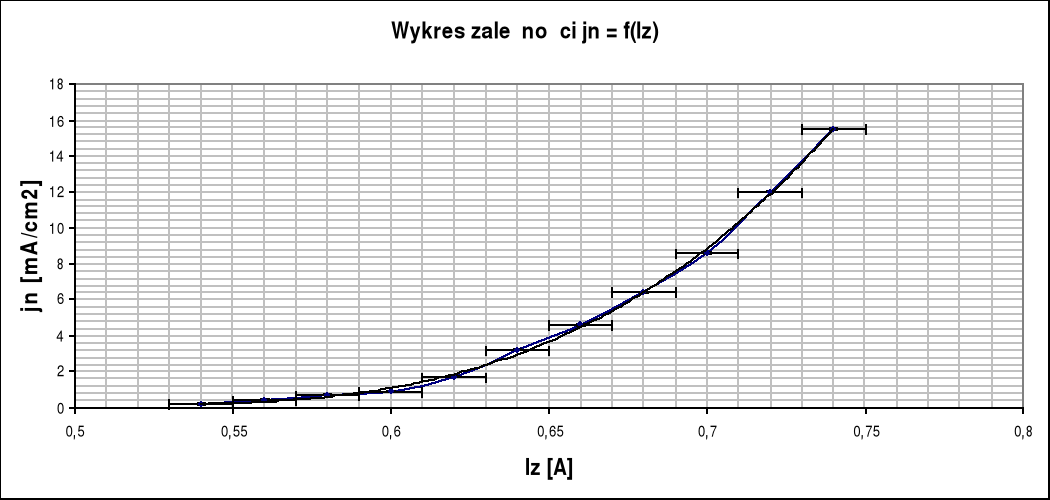
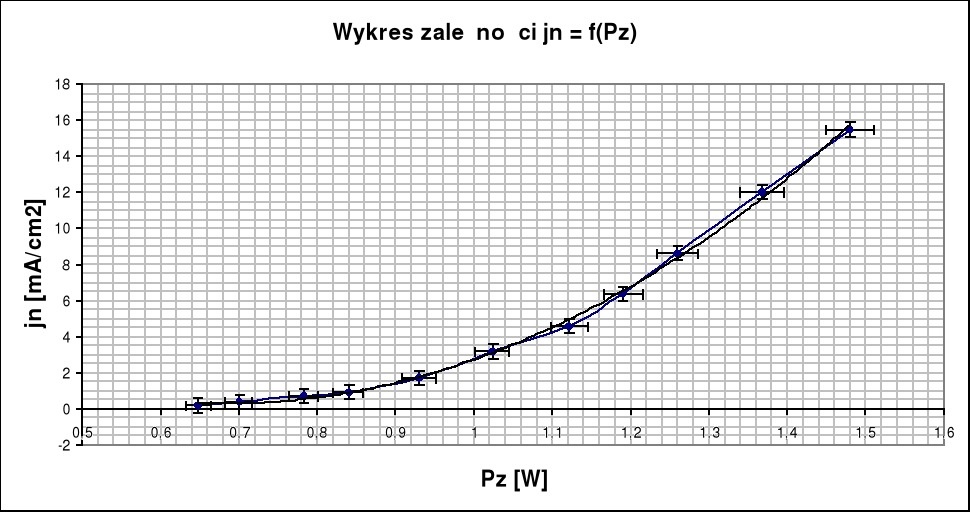
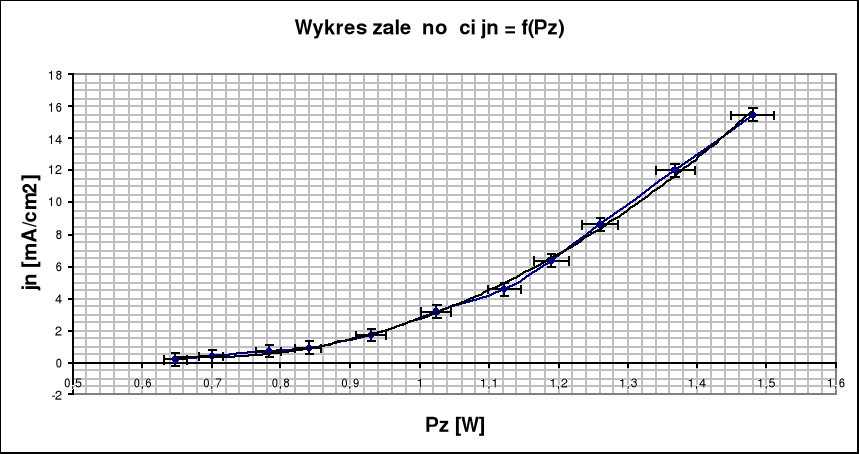
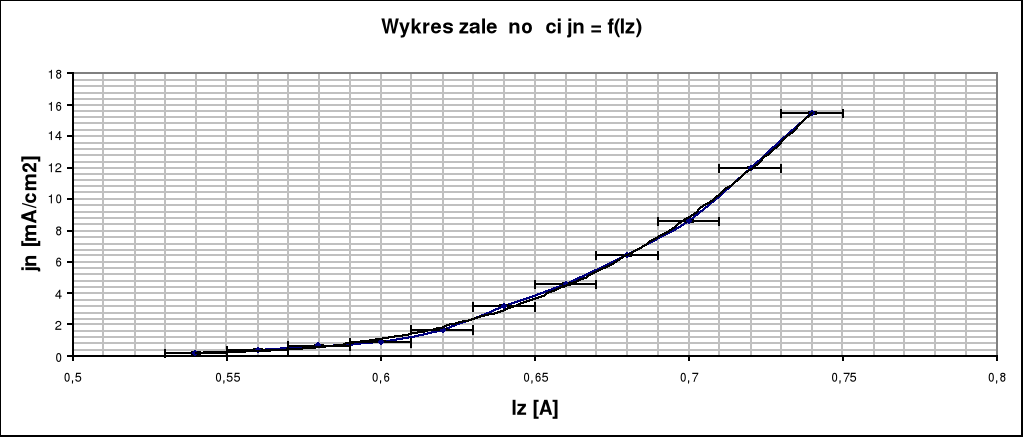
Celem ćwiczenia było zbadanie zależności natężenia prądu termoemisji od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu.
2. Schemat układu pomiarowego.
3. Ocena dokładności pojedynczych pomiarów.
Dokładność przyrządów użytych do pomiarów:
a) woltomierz analogowy: 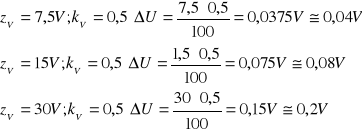
b) amperomierz analogowy: ![]()
miliamperomierz analogowy:
![]()
4. Tabele pomiarowe.
Tabela pomiarowa
Lp. |
Iż [A] |
ΔIż [A] |
Uż [V] |
ΔUż [V] |
In [mA] |
ΔIn [mA] |
1 |
0,54 |
0,01 |
1,2 |
0,04 |
0,2 |
0,04 |
2 |
0,56 |
0,01 |
1,25 |
0,04 |
0,4 |
0,04 |
3 |
0,58 |
0,01 |
1,35 |
0,04 |
0,7 |
0,04 |
4 |
0,60 |
0,01 |
1,4 |
0,04 |
0,9 |
0,04 |
5 |
0,62 |
0,01 |
1,5 |
0,04 |
1,7 |
0,04 |
6 |
0,64 |
0,01 |
1,6 |
0,04 |
3,2 |
0,04 |
7 |
0,66 |
0,01 |
1,7 |
0,04 |
4,6 |
0,04 |
8 |
0,68 |
0,01 |
1,75 |
0,04 |
6,4 |
0,04 |
9 |
0,70 |
0,01 |
1,8 |
0,08 |
8,6 |
0,04 |
10 |
0,72 |
0,01 |
1,9 |
0,08 |
12 |
0,04 |
11 |
0,74 |
0,01 |
2 |
0,2 |
15,5 |
0,04 |
Wyniki pomiarów
Pz [W] |
ΔPz [W] |
T [K] |
1/T [K-1] |
Δ 1/T [K-1] |
jn [mA/cm2] |
ln jn |
0,648 |
0,0336 |
691,4416 |
1,446*10-3 |
1,87*10-5 |
0,2 |
-1,60944 |
0,7 |
0,0349 |
704,9142 |
1,419*10-3 |
1,77*10-5 |
0,4 |
-0,91629 |
0,783 |
0,0367 |
724,9402 |
1,379*10-3 |
1,62*10-5 |
0,7 |
-0,35667 |
0,84 |
0,038 |
737,7879 |
1,355*10-3 |
1,53*10-5 |
0,9 |
-0,10536 |
0,93 |
0,0398 |
756,8023 |
1,321*10-3 |
1,41*10-5 |
1,7 |
0,530628 |
1,024 |
0,0416 |
775,241 |
1,29*10-3 |
1,31*10-5 |
3,2 |
1,163151 |
1,122 |
0,0434 |
793,1584 |
1,261*10-3 |
1,22*10-5 |
4,6 |
1,526056 |
1,19 |
0,0447 |
804,9121 |
1,24*10-3 |
1,17*10-5 |
6,4 |
1,856298 |
1,26 |
0,074 |
816,4966 |
1,225*10-3 |
1,8*10-5 |
8,6 |
2,151762 |
1,368 |
0,0766 |
833,4571 |
1,2*10-3 |
1,68*10-5 |
12 |
2,484907 |
1,48 |
0,131 |
850,0161 |
1,17*10-3 |
2,6*10-5 |
15,5 |
2,74084 |
5. Przykładowe obliczenia wyników pomiarów wielkości złożonej.
moc właściwa
wartość mocy została obliczona ze wzoru
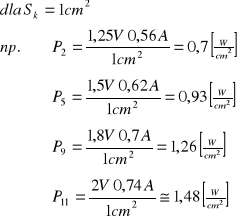
b) temperatura katody oraz jej odwrotność
wartość temperatury obliczona została ze wzoru
gdzie: ε - emisyjność całkowita równa 0,5 dla katody lampy AZ-1
σ - stała równa 5,67⋅10-12

Wartości liczbowe gęstości prądu nasycenia jn są identyczne jak wartości liczbowe natężenia prądu nasycenia In , różna jest natomiast jednostka co wynika bezpośrednio ze wzoru: .
c) praca wyjścia
Wartość pracy wyjścia obliczona została ze wzoru:
gdzie: k - stała Boltzmanna 1,38⋅10-23 [J/K]
Wartość tgα wyznaczona została na podstawie zależności:

stąd: ![]()
Praca wyjścia wynosi więc: ![]()
Pamiętając, że: mamy: ![]()
6. Rachunek błędów.
a) błąd maksymalny popełniany przy wyznaczaniu mocy właściwej został obliczony przy
pomocy różniczki logarytmicznej:
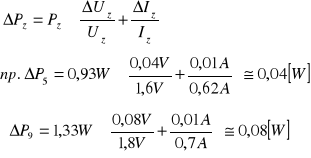
b) błąd maksymalny wartości 1/T wartości został obliczony przy pomocy różniczki zupełnej
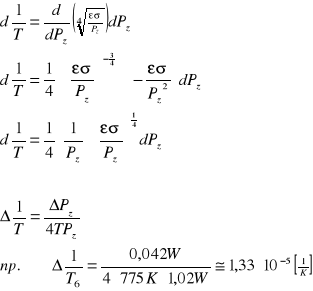
c) błąd wyznaczania wyrażenia ln jn został określony na podstawie wzoru:
pomijając błąd pomiarowy Sk mamy:
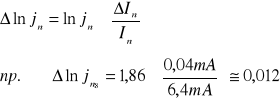
d) błąd obliczania pracy wyjścia:
Aby obliczyć błąd pracy wyjścia należało wyznaczyć najpierw błąd przeciętny
Pomiaru wartości tgα :
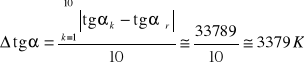
Następnie metodą np. różniczki logarytmicznej wyznacza się błąd obliczenia pracy
wyjścia:
Ostatecznie błąd wyznaczenia pracy wyjścia wynosi:
![]()
7. Zestawienie wyników pomiarów.
Praca wyjścia
Dopuszczalny zakres pracy wyjścia |
1,21 ÷ 1,77 eV |
Wartość średnia pracy wyjścia |
1,13 eV |
Pz [W] |
ΔPz [W] |
T [K] |
1/T [K-1] |
Δ 1/T [K-1] |
jn [mA/cm2] |
ln jn |
0,650 |
±0,034 |
691 |
1,4*10-3 |
±1,9*10-5 |
0,2 |
-1,61 |
0,700 |
±0,035 |
705 |
1,4*10-3 |
±1,8*10-5 |
0,4 |
-1 |
0,800 |
±0,037 |
725 |
1,38*10-3 |
±1,62*10-5 |
0,7 |
-0,4 |
0,84 |
±0,04 |
738 |
1,36*10-3 |
±1,53*10-5 |
0,9 |
-0,1 |
0,93 |
±0,04 |
757 |
1,32*10-3 |
±1,41*10-5 |
1,7 |
0,5 |
1,020 |
±0,042 |
775 |
1,3*10-3 |
±1,3*10-5 |
3,2 |
1,2 |
1,100 |
±0,044 |
793 |
1,3*10-3 |
±1,3*10-5 |
4,6 |
1,5 |
1,200 |
±0,045 |
805 |
1,2*10-3 |
±1,2*10-5 |
6,4 |
1,9 |
1,30 |
±0,08 |
816 |
1,23*10-3 |
±1,8*10-5 |
8,6 |
2,2 |
1,37 |
±0,08 |
833 |
1,2*10-3 |
±1,7*10-5 |
12 |
2,5 |
1,50 |
±0,14 |
850 |
1,2*10-3 |
±2,6*10-5 |
15,5 |
2,8 |
8. Uwagi i wnioski.
Wartość średnia pracy wyjścia elektronu z katody badanej lampy, obliczona na podstawie dołączonego do sprawozdania wykresu, wyniosła ok. 1,49 eV. Przy czym niedokładność (błąd) pomiaru tej wielkości wahała się w granicach ±0,3.
Na niedokładność pomiarów wpływ mogła mieć niestabilna wartość wielkości mierzonych wynikająca z dużej czułości elementu użytego w doświadczeniu.
Na wartość błędu wielkości mierzonych wpływ mógł mieć ewentualny błąd popełniony przez obserwatora.
Wyszukiwarka
Podobne podstrony:
63 Lampy Elektronowe, Cw 63, Rok akademicki 1996/97
51 Ładunek Właściwy Elektronu, Cw 51 , Rok akademicki 1994/95
63 Lampy Elektronowe, W63, Rok akademicki 1996 / 1997
63 Lampy Elektronowe, 63, ROK AKADEMICKI
63 Lampy Elektronowe, ĆW63 , Rok akademicki 1996 / 1997
63 Lampy Elektronowe, Fiza 63 moje, Rok akademicki
63 Lampy Elektronowe, F63, Rok akademicki : 1995/96
Cw 55, Rok akademicki 1996/97
Cw 65, Rok akademicki 1996/97
63 Lampy Elektronowe, LAB63, Laboratorium z fizyki
63 Lampy Elektronowe, CEZAR63, 1994 / 95
63 Lampy Elektronowe, FIZ63, Emisja elektron˙w z powierzchni metali ogrzanych do odpowiedniej temper
CW 23, Rok akademicki 1996/97
Elektra Cw.1, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Maszyny elektryczne
tabele i wykresy, Akademia Morska, 2 rok', Semestr III, II rok Wydział Mech, Maszyny elektryczne, Ćw
51 Ładunek Właściwy Elektronu, FIZ51 , Rok akademicki
51 Ładunek Właściwy Elektronu, FIZA 51 NASZA, Rok akademicki 1997/98
więcej podobnych podstron