1. Zasada pomiaru

Celem ćwiczenia jest zbadanie zależności natężenia prądu emisji termoelektrycznej od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu metodą prostych Richardsona.

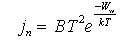
Gęstość prądu nasycenia jn - wielkość wyrażająca prąd termoelektryczny z jednostki powierzchni katody - wzrasta ze wzrostem jej temperatury. Wartość jn wyraża wzór Richardsona - Duchmana:

(1)

jn - gęstość prądu nasycenia

T - temperatura

Ww - praca wyjścia

k - stała Boltzmana

W interesujących nas zakresach temperatur, decydujący wpływ na wartość prądu nasycenia ma wykładnik potęgowy.Logarytmujac wzór (1) otrzymujemy:

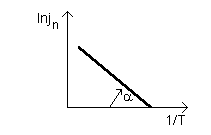
Wykresem tej zależności w układzie współrzędnych (lnjn, 1/T) jest prosta Richardsona:

Wyrażenie Ww/k jest współczynnikiem kierunkowym prostej. Z wykresu i w oparciu o wzór (2) można więc wyznaczyć pracę wyjścia Ww:

Ww = k tg

Temperaturę katody można wyznaczyć w oparciu o prawo Stefana - Boltzmana. Moc wypromieniowywana przez jednostkę powierzchni katody o temperaturze T (i jednocześnie moc żarzenia na jednostkę powierzchni katody - zużywana przez katodę na promieniowanie) wynosi:

= 5,67*10-12 W/cm2K4

= 0,5 (emisyjność całkowita lampy)

Stąd temperatura wynosi:

2. Układ pomiarowy

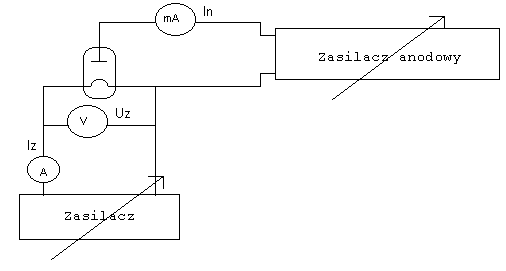
BŁĘDY WYNIKAJĄCE Z DOKŁADNOŚCI MIERNIKÓW

amperomierz (Iż) - miernik uniwersalny METEX

- zakres: 2 A

- sposób obliczania błędów pomiarowych:

1,2 % wartości wskazywanej + wartość ostatniej cyfry

miliamperomierz (In):

- ilość podziałek: 75 (zakresy: 7,5; 15)

60 (zakres 30)

- klasa dokładności: 0,5

- zakresy: 7,5 mA; 15 mA; 30 mA

woltomierz (Uż):

- ilość podziałek: 60

- klasa dokładności: 0,5

- zakres: 3

3. Tabela wyników

Sk = 1 cm²

ε = 0,5

σ = 5,67 * 10ˉ¹² W/cm²K

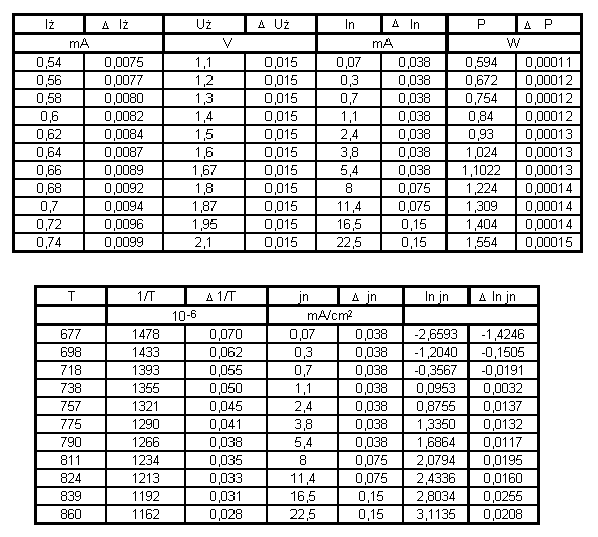
k = 1,380662 * 10ˉ²³ J/K

4. Wykres

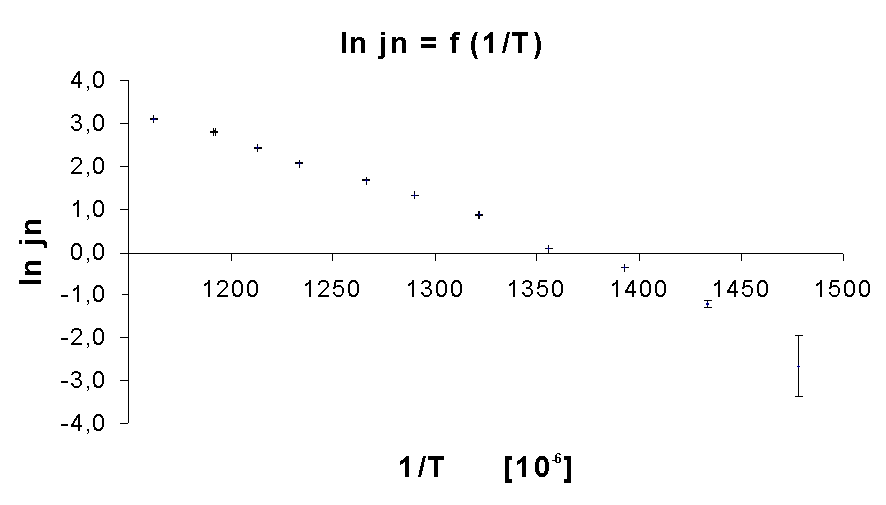
Obliczając tangens kąta nachylenia prostej w funkcji ln jn = f (1/T) do osi odciętych skorzystamy ze wzoru określonego przez stosunek wartości ln jn do wartości 1/T.

Tangensy nachylenia poszczególnych wartości wynoszą:

tg α = 7291,36

tg α = 13256,47

tg α = 21842,97

tg α śr = 14489,34

5. Obliczenie pracy wyjścia

Korzystając z obliczonych na podstawie wykresu ln jn = f (1/T) tangensów kątów prostych, można korzystając ze wzoru

W = k tg

tg1=7291,36

W = 7291,36*1,380662*10-23 = 1,0066*10-19 J = 0,6283 eV

tg2=13256,47 ⇒

W =13256,36*1,380662*10-23 = 1,8302*10-19 J = 1,14245 eV

tg3=21842,97

W = 21842,97*1,380662*10-23 = 3,0157*10-19 J = 1,88244 eV

obliczyć średnią pracę wyjścia elektronów:

k = 1,380662*10-23 J/K

1J = 6,242*1018eV

tg α = 1,4489,34 ⇒

W = k * tg α = 2,0 * 10ˉ¹°

6. Dyskusja błędów

W tabeli wyników podane są błędy przed i po zaokrągleniu. Błędy wielkości złożonych zostały obliczone metodą różniczki logarytmicznej, gdyż wszystkie one są wielkościami iloczynowymi.

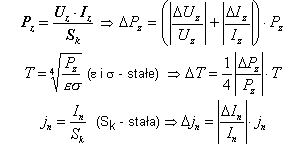
Należy zauważyć, że rozbieżność wartości tangensa kąta nachylenia prostej wynikająca z błędów pomiarowych naniesionych na wykres nie jest duża i nie wpływa znacząco na ostateczny błąd wartości pracy wyjścia.

7. Wnioski

Uśredniając otrzymane z ćwiczenia wyniki na wykresie ln jn = f (1/T) możemy zauważyć, że przebieg jest liniowy. Wynik jest porównywalny z wartościami pracy wyjścia różnych metali, podawanymi w tabelach - od 1,8 eV dla litu do 4,7 eV dla srebra co świadczy o dokładności przeprowadzonych pomiarów.

Praca wyjścia elektronu z katody badanej lampy wynosi:

Wśr = 1,25 eV

2 Marcin Domasławski. Opracowanie doświadczenia 1.

2 Marcin Domasławski. Opracowanie doświadczenia 1.

Marcin Domasławski. Opracowanie doświadczenia 1. 2

---